An Inconvenient Probability v5.6
Bayesian analysis of the probable origins of Covid. Quantifying "friggin' likely"
The most current version is now here.
[This version is substantially changed from V4 by using more relevant priors better integrated with the basic observations for simplicity. The lack of independence between when/where/what features under the lab leak hypothesis is now made explicit from the start rather than patched in. Just as I was about to post, new data on planned sequence features became available, so this update coincidentally includes not only some change in form but also an appreciable change in the odds. In 5.1 I start refining that new factor. The method remains explicitly ready for correction based on improved reasoning or new evidence.]
Introduction
Early on in the Covid pandemic, I took a preliminary look at the relative probabilities that SARS-CoV-2 (SC2) came from some sort of lab leak vs. more traditional direct zoonotic paths. Although zoonotic origins have been more common historically, the start in Wuhan where the suspect lab work was concentrated left the two possibilities with comparable probabilities. That result seemed convenient because it left strong motivation both to increase surveillance against future zoonosis and to stringently regulate dangerous lab work. Since then there have been major changes in circumstances that change both the balance of the evidence and the balance of the consequences of looking at the evidence. I think these warrant taking another look.
The origins discourse has become increasingly polarized with different opinions often tied to a package of other views. To avoid having some readers turn away out of aversion to some views that have become associated with the suspicion of a lab leak, it may help to first clarify why I think the question is important and to name some of the claims that I’m not making before plunging into the more specific analysis of probabilities.
I’m now more concerned about dangerous work being accelerated rather than useful work being over-regulated. This is not a specifically Chinese problem. Work with dangerous new viruses is planned or underway in Madison, and the Netherlands, with some questionable work in Boston. I’m not suggesting that the US or other western governments should officially say that they think SC2 started from a Wuhan lab. That would make it harder to work with China on the crucial issues of global warming and even on international pathogen safety regulation itself. (I just signed a letter “urging renewal of US-China Protocol on Scientific and Technological Cooperation”.) I’m definitely not endorsing the cruel opposition to strenuous public health measures that seems to have become associated with skepticism about the zoonotic account.
In what follows I will try to objectively calculate the odds that SC2 came from a lab, in the hope that will be useful to anyone thinking about future research policy. The underlying motivation for this effort has been eloquently described by David Relman, who has also provided a nice non-quantitative outline of the general types of evidence supporting different SC2 origins hypotheses.
Looking forward, what we really care about is estimating risks. We already know from experience that the risks of zoonotic pandemics are significant. Are the risks of some types of lab work comparably significant? We shall use some prior estimates of those risks on the way to answering a more concrete question– does it look like SC2 came from a lab? If the answer is “probably not”, then it’s at least possible that the prior estimates of significant lab risk may have been overstated, although the evidence for that would be skimpy. If the answer is “probably yes” that indicates that the prior estimates of significant risk should not have been ignored.
The method used may also help readers to evaluate other important issues without relying too much on group loyalties. The method is explicitly ready for correction based on improved reasoning or new evidence. Our method will be robust Bayesian analysis, a systematic way of updating beliefs without putting too much weight on either one’s prior beliefs or the new evidence. Bayesian analysis does not insist that any single piece of evidence be “dispositive” or fit into any rigid qualitative verbal category. Some hypotheses can start with a big subjective head-start, but none are granted categorical qualitative superiority as “null hypotheses” and none have to carry a qualitatively distinct “burden of proof”. Each piece of evidence gets some quantitative weight based on its consistency with competing hypotheses. The consistency with evidence then allows us to substantially change our prior guesses so that the final probability estimate is not just a recycling of our initial opinions.
In practice there are subjective judgments not only about the prior probabilities of different hypotheses but also about the proper weights to place on different pieces of evidence. I will use hierarchical Bayes techniques to take into account the uncertainty in the impacts of different pieces of evidence and “Robust Bayesian analysis” to allow for the uncertainty in the priors.
I am aware of 11 more-or-less-published Bayesian analyses of SC2 origins, other than my own very preliminary inconclusive one. Five of the 8 that attempt to be comprehensive come to conclusions similar to the one I shall reach here. On 1/2/2024, however, I became aware of a Bayesian spreadsheet with brief verbal comments that concluded at that time that the odds were about 3/1 favoring zoonotic origins. After I pointed out a logical error and an omission, it was modified but still somewhat favors zoonosis. I just (2/23/2024) became aware of 2 more closely linked analyses that include extensive arguments, both ending up favoring direct zoonosis. All are discussed in Appendix 1, but so far only with some sketchy preliminary notes on the last two analyses.
I will focus on comparing the probability that SC2 originated in wildlife vs. the probability that it originated in work similar to that described in the 2018 DEFUSE grant proposal submitted to the US Defense Advanced Research Project Agency from institutions that included the University of North Carolina (UNC), the National University of Singapore, and the EcoHealth Alliance as well as the Wuhan Institute of Virology (WIV). (For brevity I’ll just refer to this proposal as DEFUSE.) Although DEFUSE was not funded by DARPA, anyone who has run a grant-supported research lab knows that work on yet-to-be-funded projects routinely continues except when it requires major new expenses such as purchasing large equipment items.
I will not discuss any claims about bioweapons research. It is not exactly likely that a secret military project would request funding from DARPA for work shared between UNC and WIV.
My analysis will not make use of the rumors of roadblocks around WIV, cell-phone use gaps, sick WIV researchers, disappearances of researchers, etc. That sort of evidence might someday be important but at this point I can’t sort it out from the haze of politically motivated reports. Mumbled inconclusive evidence-free executive summaries from various agencies are even less useful. I will discuss in passing two recent U.S. government funding decisions that could potentially provide weak evidence concerning the actual probabilities as seen by those with inside information. The biological and geographic data are much more suited to reliable analysis.
The main technical portions will be unpleasantly long-winded since for a highly contentious question it’s necessary to supply supporting arguments. Although parts may look abstract to non-mathematical readers, all the arguments will be accessible and transparent, in contrast to the opaque complex modeling used in some well-known papers. For the key scientific points I will provide standard references. At some points I bolster some arguments with vivid quotes from key advocates of the zoonotic hypothesis, providing convenient links to secondary sources. The quotes may also be obtained from searchable .pdf’s of slack and email correspondence.
The outline is to
1. Give a short non-technical preview.
2. Introduce the robust Bayesian method of estimating probabilities, along with some notation.
3. Discuss a reasonable rough consensus starting point for the estimation, i.e. the prior odds for a pandemic of this sort starting in Wuhan in 2019 via routine processes unrelated to research or via research-related activities.
4. Discuss whether the main papers that have claimed to demonstrate a zoonotic origin via the wildlife trade should lead us to update our odds estimate.
5. Update the odds estimate using a variety of other evidence, especially sequence features.
6. Present brief thoughts about implications for future actions.
Preview
I will denote three general competitive hypotheses:
ZW: zoonotic source transmitted via wildlife to people, suspected via a wet-market.
ZL: zoonotic source transmitted to people via lab activities sampling, transporting or otherwise handling viruses.
LL: a laboratory-modified source, leaked in some lab mishap.
At points I’ll divide the ZW hypothesis into two branches, ZWB and ZWM, with ZWB involving direct transmission from bats and ZWM involving an intermediate host, most likely one from the wildlife trade.
The viral signatures of ZW and ZL would be similar, so the ratio of their probabilities would be estimated from knowledge of intermediate wildlife hosts, of the lab practices in handling viral samples, and detailed locations of initial cases. Demaneuf and De Maistre wrote up a careful Bayesian discussion of that issue in 2020, before the DEFUSE proposal for modifying coronaviruses was publicly known. They concluded that the probability of ZW, i.e. P(ZW), and the probability of ZL, i.e. P(ZL), were about equal.
Much of their analysis, particularly of prior probabilities, is close to the arguments I use here, but written more gracefully and with more thorough documentation. They use a different way of accounting for uncertainties than I do, but unlike some other estimates their method is transparent and rational. Here I’ll focus on comparing the probability P(ZW) to that of the LL lab account, P(LL), because sequence data point to a lab involvement in generating the viral sequence, so that P(ZL) will itself be somewhat smaller than P(LL). (I’ve added Appendix 5 to discuss the ZL probability.)
Ratios of probabilities such as P(LL)/P(ZW) are called odds. It’s easier to think in terms of odds for most of the argument because the rule for updating odds to take into account new evidence is a bit simpler than the rule for updating probabilities.
I’ll start with odds that heavily favor ZW since historically most new epidemics do not come from research activities. Then I’ll update using several important facts. The most basic what/where/when facts are that SC2 is a sarbecovirus that started a pandemic in Wuhan in 2109. Wuhan is the location of a major research lab that had not long before the outbreak submitted the DEFUSE grant proposal that included plans to collect bat sarbecoviruses and modify them in the way later found in SC2. That location, timing, and category of virus could also have occurred by accidental coincidences for ZW, but we shall see that it’s not hard to approximately convert the coincidences to factors objectively increasing the odds of LL. Here’s a beginning non-technical explanation of how the odds get updated.
I’ll start with a consensus view, that the prior guess would be that overall P(LL) is much less than P(ZW). That corresponds to the standard idea that you would call ZW the null hypothesis, i.e. the boring first guess. Rather than treat the null as qualitatively sacred I’ll just leave it as initially quantitatively more probable by a crudely estimated factor.
Now we get to the simple part that has often been either dismissed or over-emphasized. Both P(ZW) and P(LL) come from sums of tiny probabilities for each individual person. P(LL) comes mostly from a sum over individuals in Wuhan. P(ZW) comes from a sum over a much larger set of individuals spread over China and southeast Asia. Since we know with confidence that this pandemic started in Wuhan, restricting the sum of individual probabilities to people around Wuhan doesn’t reduce the chances for LL much but eliminates most of the contributions to the chances for ZW. Wuhan has less than 1% of China’s population, so ~99% of the paths to ZW are crossed off. That means we need to increase whatever P(LL)/P(ZW) odds we started with by about a factor of 100.
Further updates following the same logic come from other data. A natural outbreak could come from any of a diverse collection of pathogens, but this outbreak matched the specific subcategory of virus being studied in the Wuhan labs. Another update will come from a special genetic sequence that codes for the furin cleavage site (FCS) where the UNC-WIV-EHA DEFUSE proposal suggested adding a tiny piece of protein sequence to a natural coronavirus sequence. The tiny extra part of SC2’s spike protein, the FCS that is absent in its wild relatives, has nucleotide coding that is rare for related natural viruses but is fairly typical for the most relevant known designed sequences, the mRNA vaccines. We can again make an approximate numerical estimate of how much more coincidental the FCS and its coding seem for a natural origin than for a lab origin.
Even if we start with a generously high but plausible preference for ZW once the evidence-based updates are done we’ll have P(LL) much larger than P(ZW). P(ZW) will shrink to less than 1%, and is saved from shrinking much further only by allowance for uncertainties.
An analogy may help clarify the method for those who have never used it before. Say that you’ve been hanging out in your house for a few hours. At some point you turn on a light in the kitchen. A few minutes after that you smell burning electrical insulation in the kitchen. Even though fires are not usually caused by faulty electrical wiring in kitchens, you would rightly suspect that this one was. Bayesian reasoning allows you to systematically express and evaluate the intuitions behind that suspicion.
This openly crude and approximate form of argument may alarm readers who are not accustomed to the Fermi-style calculations routinely used by physicists. In this sort of calculation one doesn’t worry much about minor distinctions between similar factors, e.g. 8 and 12, because the arguments are not generally that precise. Sometimes the large uncertainties in such a calculation render the conclusion useless, but this turns out not to be one of those cases.
Methods
The standard logical procedure to calculate the odds, P(LL)/P(ZW), is to combine some rough prior sense of the odds with judgments of how consistent new pieces of evidence are with the LL and ZW hypotheses. Bayes’ Theorem provides the rule for how to do this. (See e.g. this introduction.)
One starts with some roughly estimated odds based on prior knowledge:
P0(LL)/P0(ZW). Then one updates the odds based on new observations. The probabilities that you would see those observations if a hypothesis (either LL or ZW) were true are denoted P(observations|LL) and P(observations|ZW), called the “likelihoods” of LL and ZW. Assuming these likelihoods are themselves known, Bayes’ Theorem tells us the new “posterior” odds are
P(LL)/P(ZW) = (P0(LL)/P0(ZW))*(P(observations|LL)/P(observations|ZW)).
In practice, it’s hard to reason about all the observations lumped together, so we break them up into more or less independent pieces, to the extent that can be done, and do the odds update using the product of the likelihood ratios for those pieces.
P(LL)/P(ZW) =
(P0(LL)/P0(ZW))*(P(obs1|LL)/P(obs1|ZW))*(P(obs2|LL)/P(obs2|ZW))…… *(P(obsn|LL)/P(obsn|ZW))
At several key points we’ll see that several aspects of the observations would not be close to independent under one or the other of the hypotheses, so we’ll be careful in those cases not to break up the likelihoods into separate factors.
At this point it’s necessary to recognize that not only the prior odds
P0(LL)/P0(ZW) but also the likelihoods involve some subjective estimates. In order to obtain a convincing answer we need to include some range of plausible values for each likelihood ratio. As we shall see, inclusion of the uncertainties is important because realistic recognition of the uncertainties will tend to pull the final odds back from an extreme value towards one.
Once our odds become products of factors of which more than one have some range of possible values, our expected value for the product is no longer equal to the product of the expected values. Since the expected value of a sum is just the sum of the expected values it’s convenient to convert the product to a sum by taking the logarithms of all the factors.
ln(P(LL)/P(ZW)) = ln(P0(LL)/P0(ZW))+ln(P(obs1|LL)/P(obs1|ZW)) … +ln(P(obsn|LL)/P(obsn|ZW)) = logit0 + logit1 … +logitn
where “logit” is used for brevity. The logarithmic form has the added advantage that the typical error bars around the best estimate are often about symmetrical.
At each stage I will include a crude estimate Li of the log of the likelihood ratio and an estimate of its uncertainty expressed as a standard error, si. Factors with large uncertainty contribute less information than do ones with similar Li but smaller uncertainty, so that in calculating the net likelihood ratio the terms with large si need to be down-weighted. The likelihood weighting technique used here is described in Appendix 3. The results are not sensitive to the details because I do not use likelihood ratios with large si. The down-weighted results are the logits used.
Once the net likelihood factor is estimated, taking uncertainties into account, we still have a distribution of plausible prior odds. This can also be treated by assuming
a probability distribution around the point estimate of the log odds. The final odds will be obtained from integrating the net probabilities, including the net likelihood factor, over that distribution. This distribution is wide enough to make its form, not just its standard deviation, potentially important for the result. The treatments of the priors and the likelihoods look superficially similar, but are not equivalent. Uncertainty in the likelihoods leads to discounting the likelihood ratios but not to discounting the priors. Uncertainty in the priors leads to discounting both. Thus observations with uncertain implications leave the priors untouched but highly uncertain priors can make fairly large likelihood ratios irrelevant. Since in this case the priors tend toward ZW but the likelihoods tend more strongly toward LL the inclusion of each type of uncertainty will substantially reduce the net odds favoring LL.
Often our hypotheses can be broken up into sub-hypotheses. For example, ZW can occur via market animals or directly from a bat, among other possibilities. LL can occur at WIV or at the Chinese CDC. There’s nothing wrong or contradictory in summing probabilities over sub-hypotheses. In calculating these contributions, however, it is crucial to separately multiply the chain of observational factors for each contributing sub-hypothesis and then add the resulting probabilities rather than adding the probabilities at each observational step and then multiplying. For example, if a hypothesis is that some cookies were stolen by a team of animals consisting of a snake and a pig knowing that that team can get through a small opening and can knock down a wall does not give any probability that they stole a cookie which could only be reached by getting through a small hole and then knocking down a wall. Neither sub-hypothesis (snake or pig) works although a coarse grained look would say that the the snake/pig team has good chances of both hole-threading and wall-smashing. This issue will come up several times in important if less extreme contexts.
Along the way we shall see several observed features that perhaps should give important likelihood factors that I think tend to favor LL but for which there’s substantial uncertainty and thus little net effect. I will just drop these to avoid cluttering the argument with unimportant factors. I will include some small factors when the sign of their logit is unambiguous, e.g. a factor from the lack of any detection of a wildlife host. I will not omit any factors that I think would favor ZW. I’ll take care not to penalize ZW’s odds for features that might seem peculiar under the ZW hypothesis but that would seem needed for a zoonotic virus to be able to cause a notable pandemic.
My analysis differs from some others in one important respect. The others treat “DEFUSE” as an observation and try to estimate something like P(DEFUSE|LL)/P(DEFUSE|ZW). I don’t see how to do that. Instead I treat DEFUSE as a way to define a particular branch of the LL hypothesis. Since it’s narrower than generic LL, it should be easier to find observations that don’t fit it, i.e. have low likelihoods. The flip side of that is that observed features that it does fit give higher likelihoods than they would for generic LL. Picking a reasonable prior for a leak of something stemming from DEFUSE-style work given the existence of the proposal will require looking more at prior estimates of lab leak probabilities rather than at the sparse history of previous pandemics. In earlier versions I used those estimates as a sanity check on more broadly inferred priors but here I switch those roles.
We will use priors based on attempts to predict yearly rates of spillovers from ongoing lab work based on prior knowledge of lab events. To the extent that those estimates are already reliable our whole exercise here is only of historical interest, since those estimates tell us directly to take lab risks seriously regardless of the source of this particular pandemic. Our priors, however, are far from precise, so looking at the evidence for this one pandemic will help us refine them. For practical purposes, we are only interested in estimating the source of this one pandemic in order to check the credibility of the warnings.
The quantitative arguments
Prior odds
Let’s start with the fuzzy generic prior odds just to get a rough feel of what’s plausible. In my lifetime, starting in 1949, there have been seven other significant (>10k dead) worldwide pandemics. At least one pandemic (1977 A/H1N1) came from some accident in dealing with viral material. So pandemics originating in research activity are not vanishingly rare. It’s more likely that the 1977 pandemic stemmed from a large-scale vaccine trial than a small-scale lab accident, so that broad background does little to pin down the prior probability of smaller-scale research triggering a pandemic. For that we need to turn to more specific studies of lab accidents.
Before looking numerically at the LL probabilities, let’s look at the competing ZW background. A tabulation from 2014 of important pathogens emerging in China since the 1950’s lists 19 different ones, including one sarbecovirus—SC1, the original SARS. From that one can roughly estimate that the probability of a significant new pathogen in any year, e.g. 2019, would be
P0(2019, ZW) = ~ 1/3.
That’s higher than the probability of some widespread disease emerging from a research incident in any year, justifying the general view that if one must choose a favored “null hypothesis” for a generic new pathogen the choice would be ZW.
Now let’s turn to lab leaks. The number of labs doing risky research has grown dramatically in recent decades. For example, Demaneuf and De Maistre show a growth of a factor of ten in the number of BSL-3 labs in China between 2000 and 2020. The book Pandora’s Gamble amply documents that pathogen lab leaks are common, including in the US. A more recent summary describes over 300 lab-acquired infections and 16 lab pathogen escapes over a two-decade period. These are almost always caught before the diseases spread. Nevertheless, in 2006, the World Health Organization warned that the most likely source of new outbreaks of the SC1 would be a lab leak, confirming that the danger of lab leaks was large according to consensus expert opinion.
There’s an important caveat, however. So far as we know, all of the past epidemics that came from labs (e.g. 1967 Marburg viral disease in Europe, 1979 anthrax in Sverdlovsk, 1977 influenza A/H1N1) were caused by natural pathogens. That’s not surprising, since until recently nobody was doing much pathogen modification in labs. The main modern method was only patented in 2006 by Ralph Baric, who was to have done the chimeric work on bat coronaviruses under the DEFUSE proposal. Without lab modification, only ZW and ZL would be viable hypotheses.
We know, however, that lots of modifications are underway now in many labs. As early as 2012, Klotz and Sylvester had warned of the dangers in a Bulletin of the Atomic Scientists article. In the same year Anthony Fauci conceded the possibility that such research might cause an ”unlikely but conceivable turn of events …which leads to an outbreak and ultimately triggers a pandemic”. The dangers were perceived as substantial enough for the Obama administration to at least nominally ban funding research involving dangerous gain-of-function modifications of pathogens.
When that ban was lifted under Trump in 2017, Marc Lipsitch and Carl Bergstrom raised alarms. Lipsitch wrote: “ [I] worry that human error could lead to the accidental release of a virus that has been enhanced in the lab so that it is more deadly or more contagious than it already is. There have already been accidents involving pathogens. For example, in 2014, dozens of workers at a U.S. Centers for Disease Control and Prevention lab were accidentally exposed to anthrax that was improperly handled.” Bergstrom tweeted a similar warning. Ironically, Peter Daszak, head of the EcoHealth Alliance, who became extremely dismissive of the lab leak possibility after Covid hit, gave a talk in 2017 warning of the “accidental &/or intentional release of laboratory-enhanced variants”.
Similar warnings came from China. In 2018 a group of Wuhan scientists, mostly from WIV, wrote “The biosafety laboratory is a double-edged sword; it can be used for the benefit of humanity but can also lead to a ‘disaster.’ ”
Perhaps the most authoritative work came from the Global Preparedness Monitoring Board which issued a prescient report from the Johns Hopkins Center for Health Security. Although that report’s many authors include at least one who has emphatically ridiculed any thought that SC2 could have come from accidental release, on Sept. 10, 2019, just before the pandemic started or was known to start, the GPMD report warned
Were a high-impact respiratory pathogen to emerge, either naturally or as the result of accidental or deliberate release, it would likely have significant public health, economic, social, and political consequences. Novel high-impact respiratory pathogens have a combination of qualities that contribute to their potential to initiate a pandemic. The combined possibilities of short incubation periods and asymptomatic spread can result in very small windows for interrupting transmission, making such an outbreak difficult to contain…’
Biosafety needs to become a national-level political priority, particularly for countries that are funding research with the potential to result in accidents with pathogens that could initiate high-impact respiratory pandemics.
It is hard to see how such warnings would make sense if expert opinion held that the recent probability of a dangerous lab leak of a novel virus was negligible. For at least the last decade the prior probability P0(LL) of escape of a modified pathogen has not been negligible.
Several relevant publications have described successful creations of dangerous lab-modified viruses. A Baric patent application filed in 2015 describes:
“Generation and Mouse Adaptation of a lethal Zoonotic Challenge Virus…. chimeric HKU3 virus (HKU3-SRBD-MA) containing the Receptor binding domain (green color) from SARS-CoV S protein. …. The asterisk indicates Y436H mutation which enhances replication in mice. HKU3-SRBD-MA was serially passaged in 20 week old BALB/c mice … to create a lethal challenge virus. “
Even more directly relevant, one paper including authors from WIV and UNC demonstrated potential for modified bat coronaviruses to become dangerous to humans:
“Using the SARS-CoV reverse genetics system, we generated and characterized a chimeric virus expressing the spike of bat coronavirus SHC014 in a mouse-adapted SARS-CoV backbone…. We synthetically re-derived an infectious full-length SHC014 recombinant virus and demonstrate robust viral replication both in vitro and in vivo.”
This paper prompted a 2015 response in Nature in which S. Wain-Hobson warned “If the virus escaped, nobody could predict the trajectory” and R. Ebright agreed “The only impact of this work is the creation, in a lab, of a new, non-natural risk.” Even in the research paper itself the authors called attention to the perceived dangers: "Scientific review panels may deem similar studies building chimeric viruses based on circulating strains too risky to pursue.” At least one paper specifically described adding an FCS to a SARS-CoV virus. The 2018 DEFUSE proposal from WIV included plans for just such modifications of coronaviruses, specifically sarbecoviruses related to SC1.
After SC2 started to spread, even K. G. Andersen, the lead author of the first key paper (“Proximal Origins”) claiming to show that LL was implausible, initially thought “…that the lab escape version of this is so friggin’ likely to have happened because they were already doing this type of work and the molecular data is [sic] fully consistent with that scenario.” That view is inconsistent with claims that the prior P0(LL) was extremely small, although it neither quantifies “friggin’ likely” nor establishes how much of “friggin’ likely” would be attributed to priors and how much to molecular data whose analysis may have since changed. Our task here will be to quantify “friggin’ likely”.
Let’s now look at some prior numerical estimates for lab leak probabilities based on records of other lab leaks. Here I will confine the LL hypothesis to one subset, leaks from research along the lines outlined in the DEFUSE proposal. In principle this omits a bit of the LL probability, but not enough to be important. From now on I’ll just use “LL” as shorthand for “DEFUSE LL”.
One serious pre-Covid paper estimated the chance of a human transmissible leak at 0.3%/year for each lab. Another careful pre-Covid analysis of experiences of labs using very good but not extreme biosafety practices, BSL-3, estimated that the yearly chance of a major human-transmissible leak was around 0.2% per lab to 1% per full-time lab worker. For a large lab doing much of its work at a much lower safety level (BSL-2) the chances would be higher. For a lab doing work on an extraordinarily transmissible virus the probability would be even higher. According to the lead coronavirus researcher at WIV, Shi Zhengli, “coronavirus research in our laboratory is conducted in BSL-2 or BSL-3 laboratories.“
A draft of the DEFUSE proposal in an early exchange among the DEFUSE team members claimed that “The BSL-2 nature of work on SARSr-CoVs makes our system highly cost-effective relative to other bat-virus systems.” The researchers specifically discussed plans to conduct work nominally described as intended to be done under enhanced BSL-3 at UNC instead in Wuhan “to stress the US side of this proposal so that DARPA are comfortable”, as Daszak put it. Ralph Baric pointed out “In China, might be growin these virus under bsl2. US researchers will likely freak out.” [sic, for multiple spots]
There were even U.S. State Department cables warning specifically that bat coronavirus work in Wuhan faced safety challenges, indicating that the Wuhan estimate should be raised compared to those for generic labs. WIV had previously demonstrated the ability to generate new strains that gave viral titers in human airway cells enhanced by over a factor of 1000 compared to the starting natural strains, ultimately leading Health and Human Services to ban WIV from receiving funding.
We can make a crude estimate that if DEFUSE-like work was started at WIV then
P0if(2019, LL) = ~ 1/100. I think that would be a major underestimate of the probability that an easily transmissible virus would leak from a BSL-2 lab working under conditions about which “US researchers will likely freak out.” I’ve arrived at that probability by implicitly considering another factor. Although WIV had previously succeeded in making a novel coronavirus with “potential for human emergence” (as had labs working with novel flu viruses) we do not know for sure that the DEFUSE plan would have succeeded in its attempt to make a human-transmissible virus. The possibility of failure needs to be factored in. My lack of expertise on that factor contributes to the large uncertainty in the priors. I would welcome estimates from disinterested virologists of the probability that a DEFUSE-like plan would not have succeeded well enough to make a problematic virus.
We do not know for sure that such work was started, but we do know that shortly after DEFUSE was turned down WIV received major funding from the Chinese Academy of Sciences for a similar but more vaguely worded proposal. Again in the spirit of crude estimates, let’s say that there’s about a 50% chance the work proceeded. We then have our starting point:
P0(2019, LL) = ~ 1/200.
This gives starting odds
P0(2019, LL)/P0(2019, ZW) = ~1/70.
Taking the log gives
L0 = ln(P0(2019, LL)/P0(2019, ZW)) = ~-4.2.
This estimate is obviously very rough, especially because of uncertainties about the lab. Let’s say that we could fairly easily be off by a factor of 10. Although each subsequent likelihood ratio adjustment has its own uncertainty, the uncertainty of these prior odds will be the most important one. Our prior is then equivalent to
L0 = -4.2 ± 2.3.
where the ±2.3, equivalent to the factor of 10, is meant to roughly show the standard error in estimating the logit. A standard error of 2.3 allows and even requires that errors outside the ±2.3 range are possible, although not very probable. “4.2” is not meant to convey false precision, just to translate our rough estimates into convenient units.
Where and What: Sarbecovirus starting in Wuhan
Now let’s take the first, most obvious pieces of evidence—the pandemic was caused by a sarbecovirus and started in Wuhan. By limiting our LL account to the DEFUSE-like subset, we’ve made one calculation trivial: P(Wuhan, sarbecovirus|LL) = ~1 since our restricted version of LL already specifies those with near certainty. In other words, LL has already paid the probability price of being restricted to a narrow version and thus avoids any likelihood cost of outcomes implied by that limited version. The more interesting question is then what’s P(Wuhan, sarbecovirus|ZW). We can make a first approximation that the location and pathogen type are independent, then refine that in more detail.
What is ln(P(sarbecovirus|ZW))? We can estimate it roughly from there being one sarbecovirus in the 19 listed emerging pathogens. Using the method described in Appendix 3, we obtain
L1 = 2.65 ± 0.8 →logit1 = 2.3.
The uncertainty is large because the ZW statistics are based on rare events, so this likelihood ratio is noticeably discounted. Again, these numbers are not meant to convey false precision. (For this term, with ln(P(sarbecovirus|LL))=0, properly separating the integrals over uncertainties in the two likelihoods would have no effect.)
What is ln(P(Wuhan|sarbecovirus, ZW))? Here things become a little more subtle because different pathogens are likely to arise in different places. We can start with a first approximation, that since Wuhan has ~0.7% of China’s population and ~1.1% of the urban population P(Wuhan|sarbecovirus, ZW) =~0.01, perhaps uncertain to about a factor of 2. That would give:
L2 = 4.6 ± 0.7 →logit2 = 4.4.
(For this term, with ln(P(sarbecovirus|LL)) not much less than zero, properly separating the integrals over uncertainties in the two likelihoods would have very little effect.)
Is there any reason to think that Wuhan would be a particularly likely or unlikely place compared to that simple population-based estimate? A recent paper working entirely within the ZW framework argues that SC2 is a fairly recent chimera of known relatives living in or near southern Yunnan, and that transmission via bats is essentially local on the relevant time scale. More detailed recent work fully confirms that conclusion. Wuhan is sufficiently remote from those locations that WIV has used Wuhan residents as negative controls for the presence of antibodies to SARS-related viruses. Thus Wuhan residents are not particularly likely to pick up infections of this sort from wildlife.
For the market branch of the ZW hypothesis, ZWM, the likelihood drops even more since it has a much smaller fraction of the wildlife trade than of the population. The total mammalian trade in all the Wuhan markets was running under 10,000 animals/year. The total Chinese trade in fur mammals alone was running at about 95,000,000 animals/year (“皮兽数量… 9500 万”). For raccoon dogs, for example, the Wuhan trade was running under 500/yr compared to the all-China trade of 1M or more, 12.3 M according to a more recent source. The Wuhan fraction was than at most about 1/2000. We can also compare the nationwide numbers for some food mammals with those of Wuhan. For the most common (bamboo rats) Wuhan accounted for only about 1/6000, apparently largely grown locally, far from sources of the relevant viruses. For wild boar Wuhan accounted for less than 1/10,000. Wuhan accounted for a higher fraction (1/400) of the much less numerous palm civet sales, but none were sold in Wuhan in November or December of 2019. It seems P(Wuhan|ZWM) would be much less than 0.01, something more like 1/1000. We may check that estimate in an independent way to make sure that it is not too far off. In response to SC2 China initially closed over 12,000 businesses dealing in the sorts of wildlife that were considered plausible hosts. Many of these business were large-scale farms or big shops. With only 17 small shops in Wuhan we again confirm that Wuhan’s share of the ZWM risk is not likely to be more than 1/1000, distinctly less than the population share of 1/100.
Future work, of which I’ve seen only preliminary versions, should separate out each different species to see what fraction of the market sales occurred in Wuhan specifically in late 2019 for species with probable SC2 susceptibility and sources near Yunnan.
The tiny fraction of the wildlife trade that is found in Wuhan means that the specific market version ZWM has much steeper odds to overcome than non-market ZW accounts would have. It will help to keep this in mind as we see further evidence that the specific market spillover hypothesis runs into other major difficulties.
Sanity Check
At this point of the analysis the combined point estimate of the logit is ~2.5 which would give odds about 12/1 favoring lab leak. When we consider how uncertain that estimate is, averaging over the range of reasonable priors, the odds would drop to about 4/1. Does that agree with other ballpark estimates?
The lead author of Proximal Origins, Andersen, wrote his colleagues on 2/2/2020 “Natural selection and accidental release are both plausible scenarios explaining the data - and a priori should be equally weighed as possible explanations. The presence of furin a posteriori moves me slightly more towards accidental release, …” Based on general priors but without specific knowledge of the DEFUSE proposal and before taking into consideration the more detailed data such as the FCS, Andersen thought the probabilities were about equal. Our odds, taking the existence of DEFUSE into account, are only a bit higher than Andersen obtained without knowledge of DEFUSE.
Demaneuf and De Maistre looked in detail at past evidence for various scenarios of natural and lab-related outbreaks. They consider ZL accounts, but the factors that go into whether there’s a research leak are largely the same as for ZW, with the difference arising more from factors we have not yet included. Without considering sequence features beyond that the virus is SARS-related they conservatively estimate that the lab-related to non-lab-related odds for an outbreak in Wuhan, P(ZL|Wuhan)/P(ZW|Wuhan), are about one-to-one. Their base estimate, for which they make no special effort to lean either way, is about 4/1. Once again we see that there’s nothing eccentric about the general range of odds we obtain just from the broadest what/when/where considerations.
The key papers arguing for zoonosis
Proximal Origins
Now let’s look at the three main papers on which claims that the evidence points to ZW rest. The first is the Proximal Origins paper, whose valid point was that ZW was at least possible. Its initially submitted version concluded logically that therefore other accounts were “not necessary”. That conclusion is implicit in all the Bayesian analyses, which neither assume nor conclude that P(ZW)=0.
The final version of Proximal Origins changed that conclusion under pressure from the journal to the illogical claim that therefore accounts other than ZW were “implausible”. To the extent that the paper had an argument for LL being implausible it was based on the assumptions that a lab would pick a computationally estimated maximally human-specialized receptor binding domain rather than just a well-adapted human receptor binding domain and that seamless modern methods of sequence modifications would not have been used. Neither assumption made sense, invalidating the conclusion. Defense Department analysts Chretien and Cutlip already noted in May 2020: “The arguments that Andersen et al. use to support a natural-origin scenario for SARS CoV-2 are not based on scientific analysis, but on unwarranted assumptions.”
The later release of the DEFUSE proposal further clarified that the precise lab modifications that Proximal Origins argued against were not ones that WIV had been planning. The DEFUSE proposal described adding some “human-specific” proteolytic site, not a special computationally optimized one, emphasizing the protease furin but also mentioning others. The particular “RRAR” amino acid sequence for the FCS that Proximal Origins argued would not have been used was identical to that of a coronavirus FCS previously studied at WIV. It is a fairly obvious candidate for a known workable human proteolytic cleavage site that works well for furin but also works for some other proteases, since as Harrison and Sachs point out: “The FCS of human ENaC α has the amino acid sequence RRAR'SVAS…that is perfectly identical with the FCS of SARS-CoV-2.” That may well be an accident, but it’s a reminder that the FCS looks similar to the sort that DEFUSE proposed. Nothing about SC2 at the level of detail of these first looks points strongly toward LL or ZW.
As further confirmation, we now know that even weeks after Proximal Origins was published its lead author did not have confidence in its conclusions or even believe its key arguments. On 4/16/2020 Andersen wrote his coauthors : “I'm still not fully convinced that no culture was involved. If culture was involved, then the prior completely changes …What concerns me here are some of the comments by Shi in the SciAm article (“I had to check the lab”, etc.) and the fact that the furin site is being messed with in vitro. … no obvious signs of engineering anywhere, but that furin site could still have been inserted via gibson assembly (and clearly creating the reverse genetic system isn't hard -the Germans managed to do exactly that for SARS-CoV-2 in less than a month.” Thus Proximal Origins contains nothing that would lead us to update our odds in either direction.
Phylogeny and location: Pekar et al. and Worobey et al.
The next papers involve phylogenetic data and intra-city location data. The likelihood factor for their combination does not factorize into separate contributions. The reason is that the locations data were used to support one particular version of the ZWM hypothesis and the phylogenetic data make that particular version implausible although on their own they would say little to disfavor the general ZW hypothesis. The core of the tension is that the viral sequences of the market-linked cases are farther from the sequences of the wild relatives than are sequences of other cases.
Pekar et al. argued based on computer simulations of a simplified model of how the infection would spread that the presence of two lineages (A and B) differing by two point mutations in the nucleic acid sequence without reliably identified intermediate cases was unlikely if all human cases descended from a single most recent common ancestor (MRCA) that was in some human. They claimed (incorrectly, see Appendix 2 ) to obtain Bayesian odds of ~60 favoring a picture in which the MRCA was in another animal shortly before two separate spillovers to humans. There is no obvious reason why getting two closely related strains from having an MRCA in some other animal a few transmission cycles before two spillovers to humans would say much about whether the other animal was a standard humanized mouse in a lab or an unspecified wildlife animal in a market. For example, multiple workers were exposed to Marburg fever in the lab and the Sverdlovsk anthrax cases included multiple strains. In the most relevant case, SARS spilled over in “four distinct events at the same laboratory in Beijing.” DEFUSE itself described planned work with quasi-species, collections of closely related strains, rather than purified strains. Thus further discussion of the Pekar et al. model seems irrelevant to our central question, but I’ll include a brief discussion in Appendix 2 about some of the major technical problems of the paper. (If there were evidence for multiple spillovers that might tend to be reduce the likelihood of the difficult direct bat to human route regardless of whether or not that involved research, as discussed in Appendix 5.)
Let’s step back from complicated, assumption-laden modeling that seems approximately irrelevant to our ZW vs. LL comparison to look at what the lineage data seem to say prima facie. (Jesse Bloom and Trevor Bedford wrote a convenient introductory discussion.) Lineage A shares with related natural viruses the two nucleotides that differ from B. Thus lineage A was the better candidate for being ancestral, as Pekar et al. acknowledged. Pekar et al. describe 23 distinct reversions out of 654 distinct substitutions in the early evolution of SC2. Naively, the chance that when two lineages are separated by two mutations (2 nucleotides, “2nt”) both those mutations would be reversions is then roughly (23/654)2 = 0.00124 = ~1/800. A more detailed calculation of the probability using data from Pekar et al. on frequencies of different reversion types gives a slightly lower value, as discussed in Appendix 2. At this point the conclusion that B was not ancestral to A tells us nothing about P(LL)/P(ZW), but it will become important when integrated with information about locations of early cases and early viral traces.
The early cases with known market linkage were of lineage B, not A. Lineage A was almost entirely absent from the main suspected site of the wildlife spillover, the Huanan Seafood Market (HSM). Although many traces of B were found in HSM, traces of A were found only on one glove, with additional mutations indicating that it was not from an early case. Thus the sequence data indicate that lineage A was quite unlikely to have originated at HSM. This conclusion applies whether or not the spillover that led to lineage A was the only one or whether there was a separate spillover to lineage B.
Both Kumar et al. and Bloom have analyzed the phylogenetic data, concluding that the MRCA was probably present in Oct. 2019, with the first spillover case likely to have occurred weeks earlier. They also believe that neither A nor B was the MRCA, which they argue differed from B by 3nt shared with wild relatives, not 2nt. There is some reason to doubt that conclusion since A differs from the main suspect by a T→C mutation, much less common at this stage than a C→T mutation, although non-reversionary mutations are much more common than reversionary ones. Bloom finds more early lineage A (and other sequences closer to their suspected MRCA) at multiple locations away from the market, including other parts of Wuhan, other parts of China, and other countries. The phylogeny data thus seem inconsistent with HSM being the only spillover site, since lineages closer to the ancestral relatives were spreading widely before the less-ancestral lineage showed up at HSM.
[3/6/2024] A thorough new Chinese paper on the phylogeny issue using the most complete data has just come out. The Zhang group finds no evidence of discontinuous evolution, i.e. they found clean sequences that are intermediate between A and B. Their existence seriously undermines the premise of Pekar et al. They conclude, contra Pekar, that a single spillover is most likely. They find four plausible candidates for the MRCA, including the two Bloom pointed to, one of which is also the one preferred by Kumar et al. They write “In sum, although multiple lineages of SARS-CoV-2 were co-circulating during the early period of the COVID-19 epidemic, they still exhibited the evolutionary continuity. All of them may have evolved from one common ancestor, probably lineage A0 or a unidentified close relative, and jumped into human via a single zoonotic event. “ No version of lineage B is included as a plausible MRCA.
The point of the Pekar et al. paper seems to have been that the absence of traces of early lineage A in HSM does not rule out the possibility that HSM was a spillover site for lineage B since lineage A could have spilled over elsewhere or perhaps also at HSM but leaving neither detected cases nor early-case RNA there. That possibility does not require that the probability of having had just one spillover is very small, just that the probability of having had more than one is not very small. Thus although the many errors in the Pekar et al. paper, discussed in Appendix 2, invalidate its conclusion that a unique spillover was highly improbable the lineage results are still at least somewhat compatible with a multi-spillover picture including one at HSM.
We’ve looked at whether the sequences found in the HSM were reasonably compatible with that being the only spillover site (they weren’t) but we haven’t made the equivalent test for WIV. Depending on what sequences were there, one could end up with a Bayes factor either favoring ZW or LL. We know that the DEFUSE proposal claimed WIV had more than 180 relevant coronavirus sequences, apparently including many unpublished ones. Unfortunately we have little information about those. Publication of newly gathered sequences seems to have abruptly stopped with those gathered in early 2016, at least according to the data I’ve been provided. (If someone knows of updates that would be helpful.) In Sept. 2019 WIV started removing public access to its sequence collection, finishing early in the pandemic. Y. Deigin discusses further omissions from public disclosure of what sequences were known as well as of when and where they were obtained. A related account of missing data has appeared in the press.
Some people consider the lack of evidence for a close match of a WIV sequence to SC2 as indicating that SC2 was unlikely to come from WIV. Others have said it’s just from reflexive bureaucratic secrecy with no particular implications. Others have read the missing-data situation as indicating a systematic cover-up of some embarrassing sequence data. Support for the latter interpretation may be found in a note dated 4/28/2020 from Daszak, a leader on the DEFUSE proposal: “ …it’s extremely important that we don’t have these sequences as part of our PREDICT release to Genbank…. having them as part of PREDICT will being [sic] very unwelcome attention…”
The official explanation of why the data base was taken offline was that it was being hacked. It seems to me that it would have been easy and inexpensive to make copies on some standard read-only media and distribute these to many dozen labs and libraries around the world. That would have made the information available without allowing hackers to modify anything without a massive worldwide conspiracy. A narrower distribution to carefully selected institutions allowing only on-site use could have not only prevented modifications but also minimized unauthorized access, although it is difficult to see why maintaining priority in using these research results would be important enough to justify the suspicions created by concealing them. An evaluation of the likelihoods under ZW, ZL, and LL of the removals of various sorts of data from Wuhan and the inconsistencies between various statements of prominent virologists would be an interesting project for a social scientist, but not one I will use to update here.
Although fully knowing what sequences were in Wuhan labs would be almost equivalent to answering the origins question, our current estimate of what’s there would mostly just be based on the other evidence leaning toward LL, ZL, or ZW, augmented a bit by a highly subjective sense of how forthright people are likely to be. We don’t want to either double-count our other evidence or introduce especially subjective terms. To summarize in more formal-looking language that some readers have indicated they prefer:
ln(P(no known backbone sequence, multiple types of hidden data|LL)/P(no known backbone sequence, multiple types of hidden data|ZW) = ~0±big uncertainty.
No update is justified.
In combining the lineage and case location data we can simplify a bit by using one point on which there is unanimity– if there were more than one spillover either all or none were lab-related. Is there evidence that lineage B spilled over to humans at HSM? If so, that would support ZWM despite its otherwise low odds due to Wuhan’s extremely small fraction of China’s wildlife trade.
The widely publicized paper by Worobey et al. used case location data to argue that HSM was not just a superspreading location but also the location of at least one spillover to humans. Worobey et al. argue that since there were hundreds of plausible superspreading locations it would require a remarkable coincidence, with probability ~1/400, for a possible spillover site, HSM, to be the first ascertained spreading site unless it were the actual spillover site. Of the major arguments (other than priors) supporting ZW, I think this is the only one that looks plausible on first inspection. While the argument sounds reasonable, one can get a preliminary empirical feel for how much of a coincidence that would be by looking at the first notable ascertained outbreak in Beijing some 56 days after initial cases were controlled. It occurred at the Xinfadi wet market, which could not have been the site of the months-earlier spillover. In Singapore, the “biggest Covid-19 community cluster” was found at the Jurong seafood market. In Thailand, the biggest outbreak was at the Mahachai Klang Koong seafood market. In Chennai, India, the biggest ascertained spread was at the Koyambedu vegetable market. Apparently first ascertainment of spread of a pre-existing human virus is not so unlikely to be located at a wet market. Given that the previous related disease, SC1, was known to have spilled over from wildlife one would expect the probability of the first ascertainment of SC2 spread in Wuhan to be even more tilted toward market cases than would that of later ascertainments, when human-to-human transmission was known. Evaluating whether the market proximity supports ZWM requires a closer look.
The case data Worobey et al. used omitted about 35% of the clinically reported known cases, perhaps ones that were not PCR-confirmed. Omission of cases can be a serious problem for an analysis based on spatial correlations. (Proximal Origins author Ian Lipkin described the Worobey et al. analysis as "… based on unverifiable data sets…") The collection of clinically reported cases and of ones then PCR-confirmed already was biased because proximity and ties to HSM were used as criteria for detecting cases in the first place. I now include in Appendix 2 a rather rigorous argument that Worobey at al. themselves present evidence demonstrating that proximity-based case ascertainment bias must have been too large to allow proximity-based inference about the origins.
Even aside from the severe ascertainment bias, re-analysis using standard spatial statistical methods by Stoyan and Chiu, experts in such techniques, showed that the statistics used could not identify HSM as the starting location. One problem was that other key sites were also inside the cluster region, including a CDC viral lab and the Hankou railway station. In addition to the more technical re-sampling statistical analysis, the re-analysis made the obvious point that in a modern city infections do not spread symmetrically in a short-range local pattern but follow other routes, e.g. commuter lines. A paper that Worobey et al. cite specifically shows extremely anisotropic movements around Wuhan, pointing out that “The intra-urban movement of individuals is affected by a number of factors, such as …mode of transportation, transportation networks….” The Hankou station is on Metro Line 2, which connects to the WIV.
Worobey et al. do not cite any relevant instance in which the sort of case-location data analysis they used identified the source of an epidemic. In the closest historical analogy I can think of, John Snow’s famous 1854 map-based identification of a water pump as a cholera source, people from infected households had walked from their houses to the pump. Even for Snow the most convincing evidence for water-borne disease causation was not spatial distribution of a cluster around the pump, subject to multiple confounders, but rather correlation with the pseudo-random spatially mixed distribution of water from two companies, only one of which was polluted. Unfortunately an analog of one of his most convincing pieces of evidence, reduction of the disease cluster round the pump right after its handle was removed, is not available for SC2. To the extent that such a temporal correlation is available, it points toward DEFUSE LL, unfortunately due to the timing of the onset rather than the timing of a reduction.
A report from the WHO and the Chinese CDC looking at the case location data concluded “Many of the early cases were associated with the Huanan market, but a similar number of cases were associated with other markets and some were not associated with any markets….No firm conclusion therefore about the role of the Huanan Market can be drawn.” That agrees with an extensive analysis by Demaneuf detailing the serious obstacles to inferring a spillover location from the sparse non-randomly selected case locations.
Worobey et al. include a map of locations of requests to the Weibo web site for assistance with Covid-like disease, which provides a way of looking at the location distribution within Wuhan without selective omission of cases. The earliest Weibo map they present shows a tight cluster near to but not centered on HSM. Instead it clusters tightly more than 3 km southeast on a Wuhan CDC site (not part of WIV) where BSL2 viral work was done. Just before the time of the first officially recorded cases the CDC opened a new site within 300m of HSM, indistinguishable from the HSM site via the sorts of case location data used in Worobey et al.
More relevant to the question of the original spillover, the paper that provided the Weibo map also had a map of Weibo data prior to 1/18/2020. By far the largest cluster of early reports in this early data set is close to the WIV on the south side of the Yangtze, as shown in this version of that map from a Senate report that includes WIV and HSM locations. Such maps cannot reliably point to the spillover site.
Worobey et al. present another argument— that the distribution of SC2 RNA within HSM pointed to a spillover from some wildlife there. If correct, that argument would be more directly relevant to whether a spillover occurred at HSM than are the locations of selected cases after Covid became more widespread.
The positive SC2 RNA reads did tend to cluster in the general vicinity of some of the HSM wildlife stalls, even after correcting for the biased sampling that focused on that area. That area, however, is also where bathrooms and a MahJong/cards room are located, both likely spreading sites. Demaneuf documents evidence from several Chinese and Western sources that the early market cases were largely of old folks who frequented the stuffy little crowded games room. A finer-grained map using the Worobey data showed the hot spot to be centered on the bathroom/games spot, although one wildlife stall is also close by.
In a short-lived coda, there were many press stories that SC2 RNA found in a stall with DNA of a raccoon dog showed that species to be the intermediate host. The presence of wildlife in the market was not news– it is implicit already in our priors. The question was whether there was some particular connection between that wildlife and SC2. When Bloom went over the actual data for the individual samples, he found that particular sample had almost undetectable SC2 RNA, far less than many others. Overall, sample-by-sample SC2 RNA correlated negatively with the presence of DNA from possible non-human hosts. In contrast, actual wildlife-infecting viruses correlated strongly positively with the corresponding DNA. A newer analysis by Bloom again indicates no support for an HSM wildlife spillover.
Thus the internal SC2 RNA data make it unlikely that wildlife had any direct connection with SC2 spread in HSM. As the head of China’s CDC concluded, “At first, we assumed the seafood market might have the virus, but now the market is more like a victim. The novel coronavirus had existed long before”. That is consistent with the prior likelihood of Wuhan being the location of a market spillover already being far less than 1% because Wuhan markets sold less than 0.01% of the Chinese mammalian wildlife trade. Nonetheless, to be conservative I will not include a Bayes factor disfavoring the general ZW hypothesis at this point, since markets are not the only path by which viruses can spillover. To express that thought in formal language again:
ln(P(market cases of non-ancestral lineage but negative internal correlation|LL)/(P(market cases of non-ancestral lineage but negative internal correlation|ZW) )= ~0 ± a bit.
Summary of Key Zoonotic Papers
Before going on to discuss other likelihood factors it may help to look back at the three papers just discussed. Regardless of whether the estimates I’m about to give of likelihood factors hold up well (one has already changed a lot thanks to discussions), the most solid conclusion is that the key papers on which the standard zoonotic story rests are extremely shaky. See Appendix 2 for more details.
Intermediate hosts
The failure to find any positive statistical association of SC2 RNA with any plausible intermediate host in the HSM points to a larger issue. For both the important recently spilled-over human coronaviruses, SC1 and MERS, intermediate wildlife hosts were found. In contrast, no wildlife intermediary has been found anywhere for SC2 despite intense searches. According to the Lancet Commission “Despite the testing of more than 80000 samples from a range of wild and farm animal species in China collected between 2015 and March, 2020, no cases of SARS-CoV-2 infection have been identified.”
Intermediate hosts were found for 3 of the 4 other recently identified human betacoronaviruses, with the missing one (HCoV-HKU1) causing a relatively minor disease that provoked relatively little attention. It would not be likely that China could have found the intermediate host for HCoV-HKU1 since retrospective evidence was found for its existence in Brazil and elsewhere years before it was first described in Hong Kong. I’ve found no indication of a search for intermediate hosts at any of those locations. A broader review of human coronaviruses finds that probable intermediate hosts have been identified for 5 of the 7 described, not counting SC2.
Given the enormous attention paid to SC2, I think the probability of not finding any intermediate under the ZW hypothesis would be less than for the other coronaviruses, but we can conservatively estimate the logarithm of probabilities consistent with the observations for the other coronaviruses. I calculate the expected value of
ln(P(no wildlife host found|ZW)) assuming a uniform prior on the probability of non-observation. (See Appendix 3) Although the identification of intermediate hosts for the two most relevant cases produces the most negative expected
ln(P(no wildlife host found|ZW)) it has large uncertainty due to the small sample. The larger samples give less negative values for ln(P(no wildlife host found|ZW)) but with reduced uncertainty. (See Appendix 3)
Of course, P(no wildlife host|LL) = 1. Thus based on the absence of any intermediate host samples expected for ZW our probabilities should be updated by a modest likelihood ratio of ~4, corresponding to:
L3 = +1.3 ±0.6 giving logit3 = 1.2.
(For this term, with ln(P(sarbecovirus|LL))=0, properly separating the integrals over uncertainties in the two likelihoods would have no effect.)
There is an interesting caveat. Wenzel has argued based on SC1 phylogeny that the market animals believed to be SC1 intermediate hosts were just secondary hosts picking up infections from humans. He argues that SC1 directly infected humans from some bat. I don’t know enough to evaluate the strength of those arguments, but if correct they would slightly increase the likelihood of failing to find an intermediate host if there were one. A bigger effect on our calculations would be to shift some of the priors away from any market story toward a direct bat story. In Appendix 5 I take a cursory look at direct bat accounts.
To be symmetrical, one should also consider whether there are any traces of an intermediate host of the type that might be found under the LL hypothesis, i.e. either cell cultures or humanized mice that would be used in the type of work proposed in DEFUSE. SC2 sequences did show up in data from the Sangon sequencing lab, which DEFUSE had named as a sequencing lab it would use, in irrelevant Antarctic samples contaminated with standard lab Vero and hamster culture cells. DEFUSE had specifically described planning to use Vero cells. The Vero and hamster mitochondrial sequences show a peculiar complementarity, suggesting the sort of cell fusion that can be induced by viral infections. Human sequences are also present. The Antarctic samples were gathered in Dec. 2019, but the contaminating lab culture samples might have been gathered later since the sequencing was done in Jan. 2020.
Three mutations that differ from the initial SC2 sequence but are shared with related wild viruses were detected in these samples, out of just 14 nt that differ from lineage B. Most strikingly, these three are just the ones that Kumar et al. assigned to the MRCA. That not only supports the Kumar et al. phylogeny but also shows that these lab samples either contained the MRCA or multiple early strains that included the MRCA nucleotides. (See Appendix 2 for details.) Unfortunately the sequences are fragmentary so it is not known if a complete MRCA sequence was present.
Comments from prominent virologists, including Bloom, Andersen, and Crits-Christof discuss possible interpretations of the data. One possibility is that the range of mutations represents an ancestral quasi-species in cell culture, for which only one or a few variants then made it through the spillover. Another is that all the SC2 RNA was obtained from multiple patients sampled in a brief time window after the pandemic was detected, and then cultured in the lab before the lab samples were sent in. Either interpretation is reasonably plausible and the second is compatible with ZW. Thus although some have cited the Sangon observation as strong evidence for LL it doesn’t let us update the odds with much confidence. Finding the main Sangon data rather than just the contaminating trace data or even just knowing the date that the samples were sent in might shed a great deal of light on the early pandemic.
Absence of ongoing spillovers
[This is a preliminary version of a new section, maybe to be revised soon.]
SC2 seems to have only spilled over once or twice. That contrasts with MERS and SC1, each with multiple spillovers. Is that a quantitative problem for ZW or just an indication that SC2 has somewhat different properties?
We do not know either the number of infected host cases or the probability of spillover per case for the ZW hypothesis. Nevertheless, we know something about what their product would have to be. By early Dec. 2019 their would be enough cases with a high enough spillover probability to make one or two spillovers reasonably likely. Market spillovers after Dec. 31 would become unlikely since HSM was shut down. At that point, based on subsequent excess deaths, there must have been roughly of the order of 10,000 human cases, i.e. more than 10 doubling times after the initial spillover(s).
If the doubling time in the hypothetical host were anything comparable to that in humans, simple exponential growth would imply that there would have to have been many spillovers before HSM was closed. That didn’t happen. There is an obvious reason why exponential growth in the hypothetical host would not have continued— there just weren’t very many host animals. The fraction infected would have saturated near 100%. That is not in itself an inconsistency in the ZW account. It does make it harder to explain why not one infected animal was found.
Although the issue of the missing spillovers has been much discussed, I’ve just started to think about it. No Bayes update is yet justified here.
Pre-adaptation
Several other simple properties of SC2 would be expected under DEFUSE-style LL but have been widely noted as surprising under ZW. Perhaps the most widely noted one was how well-adapted to humans the initial strains were, as described early on by Proximal Origins coauthor Eddie Holmes, in a communication with the others on 2/10/2020. Holmes noted this contrast with SARS-CoV-1: “It is indeed striking that this virus is so closely related to SARS yet is behaving so differently. Seems to have been pre-adapted for human spread since the get go.” Andersen noticed the same property: “what we’re[sic] observed is completely unprecedented as far as I know. Never before has a zoonotic virus jumped into humans and spread through the population like wildfire with the[sic] kind of speed.” We need to check whether those subjective first impressions were supported by the subsequent evolution of and analysis of SC2.
The initial protein evolution in humans was much slower than for SARS-CoV-1, with about a factor of 5 lower ratio of non-synonymous to synonymous mutations. The FCS region of the original SC2 also evolved little when grown in human cell cultures. The contrast with the behavior of SC1, whose natural origin is established, suggests that SC2 had already had a chance to adapt to a human cell environment, such as the human airway epithelial cells whose planned use was described in DEFUSE.
One might speculate that the slow early evolution in humans was due to some special generalized cross-species infectivity of SC2. That possibility was checked in detail by comparison with early evolution in minks after spillover from humans. The finding was again a sharp contrast between the apparent pre-adaptation for humans and the rapid evolution after spillovers to minks: “[SC2’s] apparent neutral evolution during the early pandemic….contrasts with the preceding SARS-CoV epidemics….Strong positive selection in the mink SARS-CoV-2 implies that the virus may not be preadapted to a wide range of hosts.”
The ACE2 binding site in particular worked better for humans than for bats, even before having a chance to evolve in people. As Piplani et al. noted in a Nature paper describing computational results “Conspicuously, we found that the binding of the SARS-CoV-2 S protein was higher for human ACE2 than any other species we tested, with the ACE2 binding energy order, from highest to lowest being: human > dog > monkey > hamster > ferret > cat > tiger > bat > civet > horse > cow > snake > mouse.“ The binding to human ACE2 is also substantially stronger than to raccoon dog ACE2. Although such computational estimates are not entirely reliable, in this case they correspond fairly well to observations. As noted, even in mink, for which SC2 was well-adapted, there was much more initial protein evolution than in humans. Such strong human-specific binding could result either from computationally-based selection of that region or from serial respiratory passage through lab mice with humanized ACE2 or through a combination of those.
These combined initial adaptation features, each expected for a DEFUSE-style LL but surprising for a ZW origin like that of SARS-CoV-1, should shift the odds further toward LL. Unlike some other updates, they do not easily lend themselves to semi-quantitative form but I think it is hard to see why such features would strike even expert advocates of ZW as anomalous if they were nearly as consistent with ZW as they obviously are with LL. I think that another likelihood factor
P(adaptive features|LL)/P(adaptive features|ZW) = ~3 would be conservative. I will use a small standard error only to indicate that much smaller values are implausible, not to imply that much larger values are implausible.
L4 = ~+1.1 ±0.5 giving logit4 = 1.0.
(For this informally quantitative term it wouldn’t make sense to separate the integrals over uncertainties in two likelihoods.)
Pre-adaptation combined with intermediate hosts
In treating P(adaptive features|ZW) and P(no wildlife host found|ZW) as independent factors I have made an approximation that overestimates the likelihood of ZW. A virus that circulates extensively in some post-bat wildlife has a chance to evolve from bat intestinal fecal-oral propagation to the different respiratory propagation mode found in humans, civets, etc. That possibility, however, is made more unlikely by the failure to find any proximal wildlife host. Even more surprising, no experiment has shown that any early strain of SC2 is even able to sustainably propagate in raccoon dogs or any other candidate host.
Spillover from sparse wildlife hosts is possible, but that would imply little chance for evolution since leaving bats. The combined data are then less compatible with ZW than would be calculated from a simple product of separate adaptation and host factors. This tension between the limited chances for post-bat pre-human evolution and the apparent pre-adaptation was a topic of discussion among Proximal Origins authors on 2/3/2020. Holmes wrote “No way the selection could occur in the market. Too low a density of mammals: really just small groups of 3-4 in cases.” Garry replied “That is what I thought as well…”. Holmes summed up: “Bottom line is that the Wuhan virus is beautifully adapted to human transmission but we have no trace of that evolutionary history in nature.”
Since then several bat sarbecoviruses, dubbed BANAL, have been reported to be found in Laos. Some have good human ACE2 binding although none have been found to have an FCS. Although the closest sequence of these to SC2 still differs by ~1000 nt, too much to change in the relevant time window, their existence raises the possibility that a fairly well-adapted ancestral bat virus could exist. As I discuss in Appendix 5, this could lead to a zoonotic account without tension between the lack of intermediate hosts and the good pre-adaptation because intermediate hosts would not be necessary, but in such an account ZL would be more probable than ZW.
The FCS and its neighbors
Most LL advocates have argued that the mere fact that SC2 has an FCS is strong evidence for LL since no close relative of SC2 has an FCS and DEFUSE proposed adding an FCS. As we have seen, even the lead author of Proximal Origins thought having an FCS was at least some evidence favoring LL. Nevertheless, the argument that simply having an FCS gives a major factor is exaggerated, since it would only apply to some generic randomly picked relative. SC2 is not randomly picked. We are only discussing SC2 because it caused a pandemic. So far as we know having an FCS may be common in the subset of hypothetical related viruses that are capable of causing a human pandemic. In other words even though P(FCS|ZW) is much less than one for some generic sarbecovirus P(FCS|ZW, pandemic) need not be. One needs to be cautious in using fitness-enhancing features such as the FCS in likelihood calculations. (See Appendix 4 for a consolidated discussion of how the FCS data are used here.)
Although it is not appropriate to use the non-existence of FCS’s in bat sarbecoviruses to estimate P(FCS|pandemic, ZW) the lack of an FCS in any non-bat sarbecoviruses seems to provide evidence that even though an FCS can enhance fitness in respiratory infections it’s just hard for sarbecoviruses to acquire one. The FCS of SC2 clearly has provided major evolutionary advantages for transmission in other species, yet there are no other known FCS-containing sarbecoviruses in any of the 27 non-bat species known to host sarbecoviruses. The long period of bat interactions with a range of other non-bat mammals has not produced a spillover of a persistent FCS-containing virus even though it has produced many successful spillovers. One might expect each such successful non-bat sarbecovirus to have higher probability of having an FCS than would a recently spilled-over human sarbecovirus, even one that was to go on to later have a successful career as a pandemic-causer, since these non-bat viruses have had more chances to pick up an FCS, especially by template switching with host DNA. There should be a factor disfavoring ZW based on this empirical lack of sarbecovirus FCS’s even in the face of selection pressure, but I want for now to be cautious since the presence of fairly many FCS’s in the broader category of betacoronaviruses suggests that one should not draw too strong an inference from their absence in sarbecoviruses.
Of the 27 species hosting sarbecoviruses, only 13 species have 10 or more analyzed sequences. We should probably ignore the less-sampled other species. One might estimate then that a sarbecovirus that succeeds in establishing itself in a non-bat species has a probability of picking up an FCS of less than ~1/13. The formal calculation of Appendix 3 would give an expected ln(P(FCS)|ZW)=-3.25 for zero hits on 13 tries.
What’s ln(P(FCS)|LL)? Based on DEFUSE, it seems highly likely that at an early stage of the research project some FCS would have been added. Let’s guess ~2/3 chance, i.e. ln(P(FCS)|LL)=-0.4. Then ln((P(FCS)|LL)/(P(FCS)|ZW)) = 2.8
Is this whole comparison with other species relevant? I think so but am not sure. Let’s say that their relevance is somewhere between none and complete. Crudely using a uniform distribution [0,2.8] on L5 we get
L5 = 1.4 ±0.8 giving logit5 = 1.2.
(For this term, with ln(P(sarbecovirus|LL)) not much less than 0, properly separating the integrals over uncertainties in the two likelihoods would have little effect.)
Since the presence of the FCS struck everyone from Andersen to Baltimore as suggesting lab modification, I think this modest update factor is reasonably cautious.
The specific contents of the FCS, also provide evidence. Focusing on the internal details of the FCS site is not cherry-picking statistical oddities from a large range of possibilities, since it is specifically the tiny FCS insertion that seems so peculiar for this type of virus and so predictable for DEFUSE-style synthesis. One of the Proximal Origins authors, Robert Garry, initially reacted: " I really can't think of a plausible natural scenario where you get from the bat virus or one very similar to it to [SC2] where you insert exactly 4 amino acids 12 nucleotide that all have to be added at the exact same time to gain this function -- that and you don't change any other amino acid in S2? I just can't figure out how this gets accomplished in nature. Do the alignment of the spikes at the amino acid level -- it's stunning. Of course in the lab it would be easy to generate the perfect 12 base insert that you wanted.” One particular detail of the FCS (codon usage, discussed below) initially struck David Baltimore as a “smoking gun” for LL, although he later moderated that claim.
As we saw in our introduction of the methods, rather than categorizing each unusual feature as either a smoking gun or mere coincidence, Bayesian analysis assigns each feature a quantitative odds update factor. Events that are unusual under some hypothesis do not rule out that hypothesis but they do constitute evidence against it if the events are more likely under a competing hypothesis. Our task here is to try to turn the qualitative surprise into a rough quantitative likelihood ratio.
The feature that struck Baltimore is that the SC2 FCS has two adjacent arginines (Arg’s), each coded for by the nucleotide codon CGG. CGG is the least common of the 6 Arg codons in all related natural viruses. CGG is only used for ~2.6% of the Arg’s in the rest of SC2. None of the other 40 Arg’s on the spike protein use CGG. If we treat them as approximately independent we get P(CGGCGG|ZW)= 0.0262 = ~0.0007. One can check the independence assumption for generic sarbecovirus codons using Arg pairs in closely related viruses, finding that there are zero CGGCGG’s of over 3000 ArgArg’s, indicating at best no tendency for CGG’s to pair and perhaps a tendency not to. In a broader set of relatives, the fraction of ArgArg pairs coded CGGCGG ranges from 0 outside Africa and Asia to 1/10790 in Asia to 1/5493 in Africa.
The probability of finding a CGGCGG in some generic ArgArg pair thus turns out to be very low compared to an estimate of the probability for a synthetic sequence, to be discussed below. The most favorable ZW likelihood then follows a different path, a possibility of which I was initially unaware but which a pseudonymous twitter user, “Guy Gadboit”, pointed out to me. (Gadboit will appear later with important simulations shifting the odds the other direction.) The pattern that Garry noted could be typical for a lab insertion but could also occur by a one-step natural insertion of the whole 12 nt piece. Such large insertions are not common, but when they do occur they have different codon frequencies than the rest of the virus since insertion can be read in a different frame than the source, can be reversed in direction, and has different nucleotide frequencies. Fortunately, an initial tabulation of the fraction of ArgArg’s that would be coded CGGCGG in such random long insertions has just been calculated to be 0.0158, much larger than the 0.0007 calculated from the rest of the sequence. Since the appearance of the extra 12nt piece already strongly suggested that it was a long insert, there is no need to reduce the 0.0158 much to allow for other possible evolutionary paths. We have ln(0.0158 )= -4.1, with small uncertainty compared to our upcoming estimate of the corresponding term for the LL account.
We need to compare that with an estimate of P(CGGCGG|LL). Here the argument will be less direct than for P(CGGCGG|ZW), because we don’t have a good extensive comparison set of lab insertions similar to that hypothesized for FCS under ZW. Since we will have to refine our estimate of P(CGGCGG|LL) using synthetic sequences other than viral inserts, it’s important to consider how the optimization criteria vary for different synthetic purposes and how that might affect codon use. The discussion is tedious so I’ve moved it to Appendix 4.
Given the strong indications that CGG is a popular codon for use in synthetic sequences for human hosts, I’ll assume that the purely random 1/36 is the absolute minimum estimate of P(CGGCGG|LL). As discussed in Appendix 4, there are a couple of plausible though not compelling accounts of why CGGCGG might specifically be chosen. The absolute maximum estimate is of course 1.0. We can then use the geometric mean between those limits as our consensus estimate, 1/6. Using a uniform prior on the log we get ln(P(CGGCGG|LL))= -1.8 ±1.1. Combining with our estimate for ZW gives
L6 = 4.1-1.8 = +2.3 ± 1.1 giving logit6 = 1.9
(For this term, properly separating the integrals over uncertainties in the two likelihoods would raise the LL ln(likelihood) by ~0.4 while leaving the ZW term at -4.1, giving a net logit ~2.7, i.e. favoring LL more than the value used here.)
This is far less important than the result I had initially used based on whole-sequence codon frequencies. Statistically alert readers will be suspicious on seeing another “2.3”, but this time that’s just how it came out.
The DEFUSE proposal mentions plans to modify the N-linked glycans of a natural backbone. Their fitness depends strongly on the host environment. SC2 is missing one that is found in its relatives. Further work would be needed to estimate how much that should change the likelihood ratios. It is particularly relevant for the direct bat to human route, since that would require two features (FCS and the modification of the N-linked glycan) that are unfit in bats.
Restriction Enzyme Segment Pattern
Bruttel, Washburne and VanDongen claimed in late 2022 to have identified in SC2 a pattern of segments that would be defined by cutting with the restriction enzymes BsaI/BsmBI that was characteristic of synthetically assembled coronaviruses. Unlike some other features, the restriction enzyme pattern has nothing to do with selection constraints, so its interpretation is relatively simple.
They pointed out that all the ten synthetic coronaviruses they found show a predictable restriction enzyme segment pattern, with the number of segments, Nseg, being only 5-8 and with the maximum segment length, maxL, being about 8 knt. These features make sense because using more segments in assembly is of course harder and commercial segment generators show major price increases for segments longer than 8knt. For a pair of restriction enzymes previously used together at WIV, BsaI/BsmBI, SC2 lands right in the middle of the synthetic range with Nseg = 6 and maxL being just under 8 knt. The paper argues that that pair of restriction enzymes was one of a small number of good engineering choices. Of the related natural sequences they show, only 2 out of 37 land in the synthetic range, each with 7 segments, although the 37 sequences look like they only represent about 27 independent types. Thus at first glance it appears P(BsaI/BsmBI segment pattern|ZW) = ~0.1, with our standard calculation based on 2 hits out of 27 tries giving ln(P(pattern|ZW)= -2.43±0.6.
In earlier drafts, I declined to use this in an update factor primarily because of uncertainty about how likely the pattern would be in DEFUSE-style work. Thus it was not possible to confidently calculate a likelihood ratio
P(BsaI/BsmBI segment pattern|LL)/P(BsaI/BsmBI segment pattern|ZW).
As of 1/18/2024 I became aware that Emily Kopp had obtained a draft of the DEFUSE proposal with the following passage:
We will identify the best consensus candidate and synthesize the genome using commercial vendors (e.g., BioBasic, etc.), as six contiguous cDNA pieces linked by unique restriction endonuclease sites that do not disturb the coding sequence, but allow for full length genome assembly. Full length genomes will be transcribed into RNA and electoration is used to recovery full length recombinant viruses (PMC3977350, PMC240733). Using the full length genomes, we will re-evaluate virus growth in primary human airway epithelial cells at low and high multiplicity of infections and in vivo in hACE2 transgenic mice, testing whether backbone genome sequence alters full length SARSr-CoV pre-epidemic or pathogenic potential in models of human infection.
That is exactly the assembly process that Bruttel et al. claimed to infer from examining the sequence, including the precise segment number and the “endonuclease sites that do not disturb the coding sequence”. The Bruttel et al. inference amounts to a prediction that is strikingly confirmed by the subsequent discovery of the DEFUSE draft, essentially a historical speculation subsequently confirmed by finding documentary evidence.
In a further confirmation, only one restriction enzyme is mentioned in the DEFUSE budget: “NE Biolabs R0580”. A google search turns up:
BsmBI-v2 New England Biolabs https://www.neb.com › ... › Products A Type IIS restriction endonuclease that recognizes the sequence CGTCTCN^NNNN. Replaces BsmBI (NEB #R0580).”
The other enzyme, BsaI was already in use paired with BsmBI at WIV, as described e.g. in this paper, so it is likely that for the budget large quantities of only one needed to be mentioned to describe the costs.
Given the near perfect match between the process previously inferred by Bruttel et al. and that subsequently found in a DEFUSE draft, it is hard to avoid the conclusion that P(BsaI/BsmBI segment pattern|LL) is not a great deal less than 1.
When we calculate the likelihoods of the observed pattern under LL and ZW, we need to choose how much detail to include in the pattern. In particular we need to decide whether to specify segment number Nseg=6 or allow the range 5 to 8. In general, the outcome in a Bayesian likelihood ratio calculation should be as specific as the accuracy of the observation allows, although some fuzz is acceptable if the probability has weak dependence on the observed detail. In the Bruttel et al. paper one can see that from random mutations (i.e. simulating ZW) the probability of having the maximum length maxL < 8knt falls off sharply as Nseg gets smaller. That is expected mathematically, since at Nseg=4 it becomes almost but not quite impossible to get maxL < 8knt and for lower Nseg it becomes impossible. Since the typical number of segments is bigger than 6, regardless of maxL the probability of getting 6 is lower than that of getting 7 or 8. The combined effect is large enough that one needs to include the actual observed Nseg=6 to get a good estimate of the probability of the observed result under ZW. So let’s specify the observed result more precisely and estimate
P(6, <8knt|LL)/P(6, <8knt|ZW), where the first result (6) is Nseg and the second (<8knt) is maxL.
What would be a reasonable estimate of P(6, <8knt|LL)? Although the DEFUSE draft specified Nseg=6, in practice research results often are a little different from initial plans. Furthermore, although BsmBI was specified, we don’t know for sure that BsaI would continue to be used with it. So despite the striking correspondence of the newly found DEFUSE plans with the earlier prediction, let’s cautiously estimate P(6, <8knt|LL) = ~0.1 or ln(P(6, <8knt|LL))= -2.3±0.6. (The error bars here are even cruder than the estimates, but not very important.)
Now we need to estimate ln(P(6, <8knt|ZW)). One of the authors of Bruttel et al., vanDongen, has summarized the relevant key result from their simulations: “The probability that a random 30k genome with the same nucleotide distribution as SARS2 and which was cut with BsaI and BsmBI has 6 segments and a maximum fragment length of 8kb is: 0.016%. ”
The same pseudonymous “Guy Gadboit” whose arguments and calculations led me to greatly reduce the estimate of how much CGGCGG favored LL has done simulations of how often random synonymous point mutations starting with a variety of SC2 relatives would end up with (6, <8knt), with the number of such mutations about equal to the number by which SC2 differs from each of those relatives. The largest probability for any of the starting sequences was 0.0005. Starting with a chimeric approximation to a recent common ancestor gave the next largest value, 0.00039. For one particular starting sequence whose use was urged by a zoonosis advocate, the result was zero hits in 64,000 tries. Averaging over the seven starting sequences the probability was ~0.00024, i.e. 0.024%. That’s similar to the estimate from Bruttel et al., who use a different method of simulating random sequences. Gadboit has prepared a figure illustrating how often the simulated sequences meet the maxL criterion and have different Nseg. Nseg=6 is barely visible as a slight thickening of the baseline to the left of Nseg=7.
Using these simulation estimates would give an enormous likelihood ratio, in the neighborhood of 500. I’m wary of using the simulations for absolute calibration of P(6, <8knt|ZW) especially since the natural evolution need not have proceeded by point mutations. What seems robust, however, is that P(6, <8knt|LL) is much less than P(7, <8knt|LL). My even cruder simulation, described in Appendix 3, gives that the probability of meeting the maxL<8k constraint for Nseg=6 is only about 1/8 of the probability summed over Nseg from 5 to 8. The factor of 1/8 does not include that the probability of Nseg=6 is lower than that of Nseg=7 and Nseg=8. Using these simulation estimates indicates that P(6, 8knt|ZW) should be less than P(5 to 8, 8knt|ZW) by a factor likely to be bigger than 10. Starting with the limited set of sequences shown in Bruttel et al. would then give an estimate
P(6, 8knt|ZW) < ~0.008.
A still different simulation approach, randomly picking 5 sites from the 12 relevant ones present in relatives, finds that the resulting 6-segment pattern is as uniform as in SC2 only ~0.4% of the time. Since random processes would usually also not give the observed number of segments, a substantially lower probability would be found if the Nseg result weren’t simply assigned to match observation. I’ve tried simply counting how many of the choices of 5 sites meet the maxL<8k criterion, getting 35/792. Generously allowing for maximizing P(6) from a binomial distribution by fine-tuning the expectation value then gives P(6, <8k)=0.010.
Allowing that point mutations could introduce sites outside the observed set would lower the probability further. Gadboit has shared simulation results showing that for each of the related starting sequences tried including the number of random synonymous mutation by which it differs from SC2 usually introduces extra restriction sites outside the observed set, typically~2.7 . This lowers the probability that evolutionary descent from some chimera of these relatives would give the observed pattern by a factor of ~e^(-2.7). The resulting probability of getting the observed pattern from the relatives would fall to ~0.07%, despite fine-tuning the expected number of their sites to match the observation. That’s only slightly higher than found by the two different point mutation simulations. Including this further constraint, that each site be found in a relative, would be a bit problematic, however, because it adds to the features whose probability must be subjectively estimated for the LL hypothesis.
An independent way of estimating P(6, <8knt|LL) is just to count occurrences in a large collection of related viruses, as F. Wu has done. Although Wu argued that the pattern could occur naturally, his data show that it is quite rare. Of 1316 betacoronaviruses, none except SC2 meet the (6,<8knt) criterion. Only 14 meet the broader (5-8, <8knt) criterion. For alphacoronaviruses, 4 of 1378 meet the (6, <8knt) criterion and 28 met the broader (5 to 8, <8knt) criterion. Combining the two types, one estimates P(6,<8knt|ZW) = 4/2694= 0.0015. The ratio of ones with Nseg=6 to those in the 5 to 8 range is consistent with simulations. Wu’s data also show that over time SC2 variants drifted away from the initial pattern by picking up extra sites, as one would expect if the initial form was not random.
The largest plausible estimate for P(6, <8knt|ZW) is 0.010, obtained for recombination after fine-tuning the expected number segments to 6 and ignoring the role of point mutations in creating extraneous sites, as found in both simulations and the actual evolutionary history. Simulations proceeding instead via point mutations from a putative recent common ancestral chimera give an estimate of ~0.00039. The most straightforward empirical estimate from a broad range of coronaviruses is 0.0015, near the geometric mean of the two simulation-based estimates of evolution from relatives. Thus it seems reasonably conservative to use
ln(P(6, <8knt|ZW)) = ln(0.002)= -6.3±1.1.
L7 = 6.3-2.3 = 4.0 ± 1.2 giving logit7 = 3.3.
(For this term properly separating the integrals over uncertainties in the two likelihoods would boost the net logit by ~0.3.)
Bruttel et al. raise other points that they believe are also much more likely under LL than under ZW, especially concerning patterns of synonymous mutations near the restriction sites. These arguments are more complicated and much disputed, so I won’t use them unless they get sorted out.
New Government Funding Decisions
I have not used official statements of various government agencies so far, primarily because in any country agencies have many motivations other than simply telling the public what they know. They presumably do know some things, however, beyond the public record, and that knowledge can be reflected in their concrete actions. With due allowance for other political motivations, government actions can give some evidence beyond the direct public record.
Two major U.S. agency funding decisions have come out since the first version of this piece. In one, funding for a large USAID program to sample wild viruses internationally was eliminated over concerns about “the relative risks and impact of our programming (including biosafety…)”. Since that program did not directly involve viral modifications its cancellation reflects more on ZL risks than on LL risks. Now Health and Human Services has banned WIV from receiving funding on the grounds that “WIV conducted an experiment that violated the terms of the grant regarding viral activity, which possibly did lead or could lead to health issues or other unacceptable outcomes.” Despite the delicate language the concern about possible “unacceptable outcomes” is clear. The detailed account of HHS/WIV interactions makes it clear that WIV’s secrecy about their viral work was intense enough for them to give up a significant funding source, a stronger indication of motivations than merely shutting down some public information. If these funding decisions had been made by political factions committed to an LL account, they would have no significance. Since the current administration has no such commitment, they seem to be good indications that non-public information is consistent with lab-related accounts. I’ll refrain from using them to update our odds for now, since it could be too soon to be confident about what they indicate.
Summing up
Although the point estimate of the likelihood factor ignoring uncertainties would be ~34,000,000 down-weighting due to uncertainties reduces the likelihood factor to ~4,400,000. (A more careful down-weighting separating uncertainties in LL and ZW likelihoods would give a likelihood factor of ~13,000,000) In some sense only this likelihood ratio adds any new information, since our priors were borrowed from pre-SC2 analyses. Unless one has priors of less than about 1/4,400,000, the result favors LL over ZW. The new information confirms that the prior warnings were realistic. This matters because we had little confidence that our priors were accurate.
People like to see bottom line odds that combine priors with likelihoods. Combining that likelihood ratio with the point estimate of the prior logit would still give extreme odds, P(LL)/P(ZW) = ~66,000. Integration over the range of plausible priors will bring those odds down substantially. The reason is not hard to see. If our point estimate of the logit, corresponding to P(LL) = ~99.998%, is low, raising it picks up almost no extra P(LL) because it’s already almost 100%. If on the other hand we were to lower our logit point estimate there is plenty of room for P(LL) to go down.
Let’s estimate how the uncertainty in the log of the prior odds reduces the net odds by trying some probability distributions for that log, fixing the standard deviation at 2.3. Integration (See Appendix 3) for distributions that are Gaussian, fat-tailed 3-degree-of-freedom-t, and uniform gives
Odds = 5000/1, 460/1, and 10,000/1
respectively. Due to the recent release of the detailed DEFUSE restriction enzyme segment plans our odds estimates have moved up from the middle of the previous attempts at comprehensive quantitative Bayesian estimates toward the high end. As the point estimate of the logit has gotten more extreme, the form of the distribution has become important. Most of the small chance for ZW to be true comes from the fat tail of possible misjudgments in our estimated priors.
I think roughly 500/1 is conservative because I was fairly conservative about each factor, left out some other factors that might tend to support LL, and allowed reasonable standard errors to further down-weight the likelihood factors. Nevertheless, people tend to underestimate uncertainties, so a reader might well suspect the standard errors should be larger. To get a feel for how robust the results are, we can ask what happens if we double the logs of all the uncertainty-based likelihood discounts, shift the priors down by a factor of 10, and use the fat-tailed distribution. The odds would become ~75/1. (Ironically, the main reason I’ve heard for shifting the priors down is the suspicion that the DEFUSE plan wouldn’t have succeeded.) The bottom line is just that LL looks a lot more probable than ZW, with some room for argument about exactly how much more probable. Plausible future refinements are described in Appendix 6.
The Prior Next Time
The core reason for this exercise has been to get a better estimate of how seriously to take the danger of certain types of pathogen research. It has recently been argued that the origin of SC2 has little relevance to that issue because all reasonable people agree that the danger is significant, so that one data point makes little difference. Perhaps that’s true, but in practice attitudes range from the quick assumption that the origin had to be human activity to the assumption that a direct zoonotic source remains almost certain. We tried to capture that range of attitudes with our fat-tailed distribution of priors centered around 1/70 odds that a new pandemic in China would come from a one particular risky research project rather than direct zoonosis.
We can now use the result that this pandemic was almost certainly from research activity to update the old priors to get new ones for the next pandemic. The technique is to update our prior distribution of the continuum of hypotheses for the logit x using P(LL|x)=1/(1+e-x), just as we used observations to update the probability of discrete hypotheses LL and ZW. Appendix 3 has more details. The method is identical to that recently discussed but with a wider range of priors considered. Qualitatively, the conclusion that the odds strongly favor LL just means that prior guesses that LL was highly improbable should be ignored in the future.
The result shifts our new distribution of the prior from one with a big spread centered at -4.2 (odds 1/70) to one with a bigger spread around a mean of -0.5 (odds 1/1.6). That means that for each project that is about as risky as the DEFUSE-style project the net risk is comparable to the zoonotic risk from all of China. Given the crude approximations used to get our starting prior, this should only be taken as a rough qualitative result.
Retrospective on methods
How could so many serious scientists have concluded that P(ZW) is not only bigger than P(LL) but even much bigger than P(LL)? There was of course a great deal of intensely motivated reasoning, as the internal communications among key players vividly illustrate. Some important evidence (e.g. re the restriction enzymes) was not available until after many had already formed opinions. For those just following the literature in the usual way, the impression left by the titles and abstracts of major publications suggested that ZW had been repeatedly confirmed although we’ve seen that the arguments in the key publications disintegrate or even reverse under scrutiny. When major errors were found in the key papers, the authors resisted making even mathematically necessary corrections, in contrast to what I’ve tried to do here.
There has also been a familiar methodology problem among the larger community that accepted the conventional conclusion. Although simple Bayesian reasoning is often taught in beginning statistics classes, many scientists have never used it and fall back on dichotomous verbal reasoning. The story that’s initially more probable, or at least more convenient, is given qualitatively favored status as the “null hypothesis”. Each individual piece of evidence is then tested to see if it provides strong evidence against the null. If the evidence fails to meet some high threshold, then the null is not rejected. It is a common error to then think that the null has been confirmed, rather than that its probability has been reduced by the new evidence. After a few rounds of this categorical reasoning, one can think that the null has been repeatedly confirmed rather than that a likelihood ratio strongly favoring the opposite conclusion has been found.
What should be done?
Despite prior probabilities favoring zoonosis we have seen that after evidence-based updating the odds strongly favor a lab leak origin. Thus it was wrong to dismiss prior warnings of lab risks. How might that inform our actions?
Blaming China is about the most counterproductive possible reaction. The lead Proximal Origin author, Andersen, alluded to the dangers of such blame when on 2/1/2020 he asked his colleagues: “Destroy the world based on sequence data. Yay or nay?” We’ve now seen what the sequence data say but we don’t want to destroy the world— just the opposite. We need to regulate pathogen research in ways that avoid the most dangerous work while expanding work needed to develop vaccines and therapies. No new ideas are needed for the guidelines, since in 2018 Lipsitch already outlined exactly the sort needed to achieve those goals. Meanwhile, paying attention to lab risks cannot be an excuse to ignore ongoing zoonotic risks, since even if this pandemic probably came from a lab we know that others have been zoonotic.
Reflection
None of the three clear existential threats to humanity– global warming, new pathogens, and nuclear war– can be addressed without science. I think that some public trust in science is a necessary though not sufficient condition for successful defenses against those threats. For example, public awareness of the scientific conclusion that SC2 mainly spreads by aerosols and of the value of indoor air filtering would have limited and still could limit the disease burden. When scientists are not candid about what we know we undermine the necessary public trust.
Appendix 1: Other Bayesian analyses
An anonymous twitter user has posted a handy Bayes calculator that readers can use to make their own estimates. It is suited only for straight Bayes calculations. In order to realistically allow for uncertainty in the factors users will need to try various combinations of plausible values and then take a weighted average of the resulting probabilities, not of the resulting odds, to get their best odds estimate. Averaging the odds themselves gives an over-estimate.
Demaneuf and De Maistre’s Bayesian analysis, written before DEFUSE or the published WIV sampling in Laos were known and omitting sequence considerations, provides a useful introduction to the form of the arguments, as well as detailed analyses of the priors. Readers who find something confusing about basic Bayesian reasoning may find their “rebuttal of common misunderstandings” particularly useful.
A brief Bayesian analysis by J. Seymour only considering priors and geographical factors (like my early one) came out in Jan. 2021. It considers a range of possible values obtaining estimates of lab leak probability ranging from 0.05% to 91%. The biggest difference from my current analysis is that Seymour uses no biological data, but he also mostly uses lower priors, without empirical explanation.
In Feb. 2021 Latham and Wilson published a discussion of how unlikely it would be for a natural sarbecovirus to first show up in Wuhan. They do not include a quantitative estimate for a lab leak probability for comparison, but their discussion makes it clear that they consider some form of lab leak far more probable. In March 2021 Brunner followed up the previous works with an analysis also focusing on geography plus knowing the pathogen was a sarbecovirus. He obtained a lab leak probability of 69%, quite close to our value at the same point in the analysis, as described in the “sanity check” section above.
Tuntable has written a summary of a variety of lines of evidence, for the most part parallel to the argument I’ve presented. The spirit is Bayesian but few of the pieces of evidence are assigned quantitative values. The conclusion is similar to the more explicitly Bayesian analyses.
The first fairly comprehensive Bayesian analysis that took geographical, biological, and social factors into account came out in 2020 from “rootclaim”, a project led by Saar Wilf. It concluded that some lab event is about thirty times as likely as a pure zoonotic wildlife scenario. That analysis contains a wealth of useful references and discussion but is a bit out of date and uses a method of accounting for uncertainties in the factors that is specialized to distributions of logits that consist of a component at zero and another sharply defined component at another value. In practice most of the relevant factors have fuzzy unimodal distributions.
Recently rootclaim held a lengthy organized high-stakes oral debate with Peter Miller on whether their conclusion was right. Miller won- i.e. the two judges thought that zoonosis was more likely based exclusively on the debate. I’ve watched a few hours of that 18-hour debate, focussing on parts recommended by Miller. Now both judges have posted written summaries of their reasoning, even longer than my arguments here. I’ll put my first fragmentary thoughts about their summaries at the end of this Appendix, with more complete responses to come later, as time permits.
An extraordinarily detailed analysis from early 2021 by S. Quay concluded that the probability of a lab leak origin was 99.8%, i.e. 500 times as likely as pure zoonosis. (I had forgotten hearing of Quay’s paper until after I finished the core analysis of this paper, so the detailed analyses are independent.) Although there is overlap with my analysis, Quay’s mathematical treatment does not follow a systematic logical system, as Andrew Gelman noted.
Louis Nemzer tweeted an analysis on 10/28.2021 that used straight Bayesian methods rather than robust Bayes, i.e. did not include uncertainties on the factors. This analysis is particularly compact and easy to follow. It includes priors that are somewhat less favorable to LL than mine, a larger factor than I use for the existence of the FCS, and a larger factor for the CGGCGG. He does not include factors for non-observation of hosts or for pre-adaptation. Nemzer ends up with 1000/1 odds favoring LL. Those odds are similar to those I get before averaging over the distribution of plausible priors.
An anonymous twitter user posted a brief Bayesian evaluation on 6/20/2022 with fairly much overlap with mine, also concluding that a lab leak was much more probable than competing hypotheses. They used the presence of the FCS to an extent that I think is not justified, but they do not get around to using some other details of the genomic sequence that I find to be important.
In Nov. 2022 Alex Washburne posted a well-written Bayesian analysis that includes several pieces of useful auxiliary information (e.g. alternate funding sources for the work) that I do not cover much here. He does not provide a numerical summary, but implies odds stronger than I obtain. As in most other analyses, he uses the existence of the FCS as evidence in a way that I argue fails to condition on the existence of a pandemic. Uniquely, Washburne includes his work done with Bruttel and VanDongen, work that was much derided and that I had not considered quite robust enough to use. In light of a recent further DEFUSE release, I have finally included a version of that argument here.
David Johnston has posted a Bayesian spreadsheet with odds currently (1/6/2023) favoring zoonotic origins. When first posted it omitted any LL-favoring factor for missing hosts on the grounds that the disease could have come straight from bats but inconsistently also included a ZW-favoring factor due to proximity to HSM non-bat hosts. The CGGCGG factor was mentioned but not included. Repairing these two flaws using his conservative estimates would have raised the odds to a little more than 5/1 favoring LL. The newly posted version, however, includes several other changes each favoring ZW, so that the estimated probability of ZW only drops from 0.7467896541 to 0.6781080632.
For now I will mention only a few of the problems I see with Johnston’s analysis. One of the new changes was to reduce an FCS factor from 5.0 to 2.5, with no explanation, thus minimizing changes in the bottom line. A factor of 1.5 favoring ZW is now included based on the lack of an explicit statement in FOIA documents acknowledging a lab leak. I think that is a peculiar way to interpret statements such as Andersen’s “that the lab escape version of this is so friggin’ likely to have happened because they were already doing this type of work and the molecular data is [sic] fully consistent with that scenario” and Daszak’s ” having [the sequences] as part of PREDICT will being [sic] very unwelcome attention…” as well as many other statements along the same lines. Johnston includes a factor of 8 from HSM/Worobey effects, including a factor of 2.5 favoring ZW due to “proximity to wild animals” inside HSM. Given that SC2, unlike other coronaviruses, failed to show any association with potential host species, that seems like another peculiar read, perhaps even upside down. The contrast of seeing those data as positive evidence of association while seeing the FOIAs as negative evidence for lab problems is striking. There are numerous other issues, including some double-counting, but these give a flavor for why Johnston’s results differ from the others.
The two rootclaim debate judges, Eric Stansifer and Will Van Treuren posted independent analyses of the evidence presented in the organized debate in which they jointly participated, sharing responses to questions, etc. I have major disagreements with both analyses, including on basic methods. For now, I’ll just describe some key points. These comments may be extended and perhaps modified when I get a chance to look over these analyses more carefully. I will use first names here, following the convention used by the debaters.
Both Will and Eric derive by far their strongest ZW-favoring factor from the first ascertained spreading site being HSM. Neither use my new argument showing that Worobey has strong internal evidence of ascertainment bias. Neither uses CDC-head Gao’s acknowledgment that the initial search was heavily biased.
Neither Will nor Eric uses the recent re-examination of the restriction enzyme site pattern prompted by Kopp’s publication of the detailed DEFUSE plans for those, matching the observed results. I think these may have only become available after the debate. They do provide a significant LL-favoring factor.
Both use probabilities P(Wuhan|ZW) based pretty closely on population, but then use the HSM-based data to obtain by far the biggest ZW-favoring factor. This misses the key point about sub-hypotheses— the HSM results can only be used to boost the market-based sub-hypothesis of ZW, but the Wuhan wet markets got far less of the relevant animal trade than would be expected from the population fraction. One cannot multiply an inter-city likelihood of one sub-hypothesis with an intra-city likelihood of a disjoint sub-hypothesis to obtain the net likelihood of the overall hypothesis. It’s odd that so little attention has been paid in other analyses to how little of the wildlife trade makes it to Wuhan compared to the enormous country-wide trade, as I discuss above.
I’ll briefly discuss Eric’s analysis first. I’m not sure this will matter in the end but after an unusually clear explanation of what frequentist p-values mean and an acceptable description of Bayesian reasoning, Eric gives a flawed description of how they are connected. Bayesian likelihoods are not p-values and the ratio of likelihoods is not the ratio of p-values. (Eric’s follow-up response makes it clear that this was a deep misunderstanding and lack familiarity with Bayesian methods, not just careless writing.)
With regard to the bottom line, Eric includes a likelihood factor of 10,000 based on the Worobey HSM location data. We have seen strong evidence that the case location data was severely biased. Bloom showed that the internal HSM nucleic acid correlations lacked the signature found for actual animal corona viruses. The market-linked cases are all from a lineage the recent through Chinese research shows is not ancestral, as Blomm and Kumar had earlier inferred from less complete data. Just common sense would say that the chance that Chinese authorities would initially distort the available data to support the market hypothesis over the LL hypothesis was far larger than 1/10,000! Could anyone seriously claim that chance was much smaller than 1/10? The issue is analogous to the one I ran into for the LL-favoring CGGCGG factor. A very large odds calculation can be obtained within a narrow model. Both nature and people have ways of stepping around the narrow models, giving much lower odds. Eric also includes a probability of 1/50 for WIV even attempting DEFUSE-like work, This seems strangely low, completely in disagreement with the universal reaction of the Proximal Origins authors and their correspondents even before they knew of the DEFUSE proposal. (In the comments below, it appears that about a factor of 10 of this comes from the low probability of the resulting virus being as nasty as SC2. From discussions with experts, I don’t think that the probability of particular nastiness is predictably different between DIFFUSE-style lab and natural viruses that have passed the transmissibility threshold. Presumably bioweapon pathogens would be nastier, but there’s no indication that anything like that was involved.) Without worrying about other factors, just bringing these two factors into something even close to a reasonable range (say 1/5 for the work going ahead, 1/10 for the Worobey data coming from selective ascertainment and presentation) would swing Eric’s final odds to favoring LL by about a factor of 8.
The general form of Will’s arguments feels more compatible with a Bayesian approach than does Eric’s. Will provides a useful spreadsheet summary of his Bayesian factors, which together with his priors give odds ~275/1 favoring ZW. He also uses an extreme likelihood ratio for the HSM data, 1000. Again, this factor simply assumes that there are no major problems with the Worobey data despite strong evidence of problems. Allowing even an unrealistically low probability (0.1) for the data problems to give rise to the appearance that the market origin hadn’t been preceded by pretty much prior spread would shift the odds by a factor of 100. Will also uses a probability of 0.01 for WIV having a backbone sequence sufficiently close to SC2. This calculation seems to assume that under LL WIV needed to search its database for a near-match to a pre-determined SC2 backbone rather than that the SC2 backbone was chosen from or assembled from whatever was in the available collection of unpublished sequences. At least on first reading, it seems to be an example of the common statistical error exemplified by seeing a license plate at a crime scene and arguing that the probability of that exact license plate being that of a suspect are extremely low. Reducing this unreasonable factor to something more logical would again leave odds favoring LL.
Appendix 2: Worobey et al. and Pekar et al.
Worobey
Arguments about how much weight to put on anecdotal evidence for or against strong proximity-based ascertainment bias are unlikely to be persuasive. I have noticed, however, that the Worobey et al. paper includes internal evidence that shows rather conclusively that there was major proximity ascertainment bias. The argument that follows is my only original contribution to the origins dispute.
Let’s consider two hypotheses, W and M. W is that all the cases ultimately come from the HSM and that fact accounts for the observed clustering near the HSM, with no major ascertainment bias. M is that the proximity ascertainment bias is too large to allow inference about the original source from the location data. These hypotheses have opposite implications for the correlation between detected linkage to HSM and distance from HSM.
For hypothesis W there is some typical distance from HSM to a linked case. An unlinked case must come from a linkable case (typically not observed) via some additional transmission steps in which the traceability is lost. The mean-square distance (MSD) to HSM of the unlinked cases would then be the sum of the MSD of the linked cases and the MSD of the remaining steps in which traceability was lost. Barring some peculiar contrivance, the unlinked cases are then on average farther away from HSM than the linked cases. The linkage-distance correlation is negative.
For hypothesis M case observation can arise either via linkage or proximity. Some cases are found by following links, others by scrutiny near HSM. Observation is a causal collider between linkage and proximity: linkage→observation←proximity. Within the observed stratum of cases collider stratification bias then gives a negative correlation between linkage and proximity, i.e. a positive linkage-distance correlation.
The relevant observational results are reported clearly by Worobey et. al. “(ii) cases linked directly to the Huanan market (median distance 5.74 km…), and (iii) cases with no evidence of a direct link to the Huanan market (median distance 4.00 km…. The cases with no known link to the market on average resided closer to the market than the cases with links to the market (P = 0.029).” The statistical significance of the deviation from the W hypothesis is even stronger than the “p=0.029” would indicate since that calculation was for the hypothesis of no difference but W implies a noticeable difference of the opposite sign. Thus the W hypothesis is disconfirmed by the data of Worobey et al. The sign of the linkage-distance correlation instead agrees with the M hypothesis, that there is substantial proximity-based detection bias.
Since the reports of the early cases included a claim that there was no evidence of human-to-human transmission, the linked cases must almost all be directly linked with the patients themselves having been at the market. Unlinked cases, in contrast, could easily be more than one transmission step away from their last linkable ancestor. Although the typical relative displacement of a unlinkable step is not known, that there are typically at least as many such steps as of the direct linkable ones strengthens the case that the unlinkable cases should be appreciably farther from HSM than the linked ones if W hold.
Under W one would also expect the more distant unlinked cases to be displaced in roughly the same directions as the linked cases from which they descend. Visual inspection of the map of linked and unlinked cases, their Fig. 1A, does not support such an interpretation since the linked cases tend to be north of HSM and the unlinked south and east. Quantitatively, using the case location data from their Supplement one finds an angle of 105° between the displacements from HSM to the centroids of the linked and unlinked cases, i.e. a slightly negative dot product between those typical displacements. That would be surprising for any account in which cases start with a linkable market transmission and then at some point lose linkage through an untraceable transmission.
Worobey et al. do propose a distinction between types of linked cases that could in principle lead to difference in distances between linked and unlinked cases. They point out that cases linked because the patient (or a linkable contact) worked at HSM might typically be farther than ones linked via shopping at HSM. They do not directly explain how that heterogeneity within the linked cases would give a distance contrast between linked and unlinked cases. In order for that difference to show up as the observed effect one would need to add another assumption, that it would be harder to trace secondary connections to the nearby shoppers. No explanation is given for why such an effect would be expected or for what sign it would be expected to have. One might expect that among people near the market it would be easier to find contacts with neighbors with linked cases. A second-order explanation along these lines remains in the realm of possibility although more speculative than the simple first-order observational collider bias.
The combination of the direction and typical distance observations is especially hard to reconcile with W. That the more distant unlinked cases are displaced in an entirely different direction than the linked cases would require that their unlinked steps be even larger than the earlier linked steps. That sits awkwardly with the requirement that overall the unlinked steps be so small that some correlation between their existence and some internal diversity of the linked steps accounts for their greater proximity to HSM.
The probable existence of major proximity detection bias should not be taken to imply that there is no actual clustering of the unlinked cases. It just means we have no reliable way of knowing if there is.
Pekar
Although as we’ve seen the question of whether there were two spillovers or one has little or no general direct relevance to LL vs. ZW, the absence of the more ancestral lineage A from HSM fits poorly with the HSM version of ZW unless there were multiple spillovers. Thus despite its limited general relevance a good deal of attention has been paid to the argument of Pekar et al. that there were two spillovers.
Pekar et al. use a Bayesian calculation to infer the probability that there were two spillovers rather than one based on the later phylogenetic pattern. Although the Pekar et al. phylogeny contradicts analyses based on more complete data, it’s worth looking at it in detail just to get a further feel for the reliability of major work in this field. We’ve seen that calculating Bayesian odds involves both picking priors and calculating likelihood ratios. The priors used by Pekar et al. are peculiar even on superficial inspection, but not by a huge factor, but the likelihood ratios used have multiple serious mathematical errors.
The Bayesian analysis of Pekar et al. calculates conditional probabilities of different observations for the N=1 and N=2 hypotheses, with more specific results required for N=1. Specifically, only the N=1 hypothesis is required to give “the mutation separation and relative clade size”. That the mutation separation for N=2 is not required to fit the observed 2 nt gives a particularly severe imbalance. That imbalance is certain to bias the results toward N=2, but by how much is not yet known.
Three pubpeer analyses find multiple errors in the code used to calculate the likelihood ratio. One error seems to be due to a simple copy-paste mistake. The next is somewhat more conceptual, an incorrect normalization of the likelihoods. Together those two “combined corrections reduce the Bayes factors from ~60 to less than 5.” The third is a double-counting error: “Removing the duplicated likelihoods reduces the Bayes factors by a further ~12%.” A numerical correction for these three coding errors has belatedly been included in the Science paper, although without changing any verbal results or acknowledging that the errors were discovered by a pubeer contributor. In order to verbally accommodate the reduction in the Bayes factor from ~60 to ~4.3 the revised version drops the minimum cutoff for “significance” from 10 to 3.2. The full story is recounted by Demaneuf.
Oddly, after much complicated error-prone model-dependent analysis of the likelihood ratio for two spillovers vs. one spillover the prior odds were just arbitrarily assigned to be 1.0. (See page 13 of the Supplement to Pekar et al.) In effect the prior probabilities used for N, the number of successful spillovers, were P(1) =1/2, P(2)=1/2, P(3)=0, P(4)=0, etc. Let’s assume, pretty realistically, a Poisson distribution for N with expectation value x. There is no value of x nor is there any probability distribution of x that leads to the set of prior probabilities use by Pekar et al. Thus it looks like a post-hoc attempt to inflate the prior probability of N=2.
We don’t know x but it can’t be very small because then no spillovers would have been found or very big because then even more than two would have been found. A standard non-informative form for the prior probability density function of x is 1/x. Its integral diverges weakly but that divergence will not affect the odds. We can then easily integrate the Poisson probabilities over x to get the prior odds, P(N=2)/P(N=1) = 1/2. These conventional non-informative priors would reduce the resulting posterior Bayes odds from ~4.3 to ~2.2. It is peculiar that the paper did not use such a conventional exercise to obtain the prior odds without post-hoc adjustment.
Since we require N>0 to observe a pandemic the probability density of x for observed cases excludes the N=0 cases, leaving a distribution of the form (1-e-x)/x, eliminating the small-x divergence. This does not change the odds since those excluded N=0 cases did not contribute to the odds. Extension of this method to higher N gives a very weakly divergent sum of probabilities that stays finite if truncated, e.g. at N= population of Wuhan.
The pseudonymous author “Nod Nizzaneela” who posted the major coding errors (now acknowledged) on pubpeer now reports that there is another small error in the same direction. Even without correcting for that error, rerunning the code reduced the likelihood ratio of the main estimate to 3.5, which would give odds of 1.8 when combined with conventional priors. 1.8 is less than the revised significance cutoff of 3.2. Of course, it would always be possible to choose a lower cutoff if needed. That 1.8 still includes no correction for the fundamental imbalance in the conditional likelihood conditions used for N=1 and N=2.
In a recent personal communication with respect to the issue of unbalanced requirements for N=1 and N=2 Nod confirms “The simulations contain neglected information that can inform the likelihood of two introductions satisfying the full conditions. Preliminary calculations that combine this information with non-informative priors for the source diversity indicate that the fraction of the N=2 results that meet the full conditions required of the N=1 results is low enough to reduce the Bayes factor to less than 1. These results are preliminary." In the latest communication from Nod, he has added the requirement that the N=2 case meets the same condition on the relative weights of the two polytomies that was required of the N=1 case: “instead of taking the likelihood of two successful introductions having two basal polytomies as the likelihood of one having one, squared, I draw random pairs from my simulations, with replacement, and test for basal polytomies and relative size.”The t
The remaining small effect (of unknown direction, but probably favoring N=1) depends critically on the quality of the epidemiological model. Fundamental problems with the model have been noted. The simplifications used in the model have been described as strongly inappropriate for SC2, with arbitrary and likely unrealistic probability distributions of spreading events. As S. Zhao et al. wrote re Pekar et al.: “In the coalescent process of their simulations, they assumed that viruses spread and evolve without population structure, which is inconsistent with viral epidemic processes with extensive clustered infections, founder effects, and sampling bias” Omitting the blotchy population structure of transmission and blotchy ascertainment probability in location and time severely loosens the connection between the model and real data. Since having a non-ascertained early phase in a distinct population (other host species) introduces just the sort of realistic elements that were left out of the over-simplified model, it is no surprise that the model fit could be improved by inclusion of these features via the hypothesized multiple spillover. These model problems affect not only the topology odds but also the estimated time to the MRCA.
Whether a properly done version of the Bayesian modeling exercise in Pekar et al. would leave P(N=2) or P(N=1) larger is not clear, although it is clear that N=2 could not be strongly favored. Since whether N=1 favors LL or ZW is also unknown this conclusion would not lead us to change our P(LL)/P(ZW) odds even if the phylogeny account had not been been contradicted by ones based on more complete data.
With regard to the MRCA, Pekar et al point out that most reversionary mutations (regardless of which MRCA is picked) are of the C→T form. 19 distinct such mutations were found in the 787 early sequences they describe. Only 4 other distinct reversionary mutations from lineage B were found, or 3 from lineage A. The C→T mutations often showed up more than once–I count 41 times in their Figure 1. Non-reversionary mutations also occur more than once, with the total mutation count running about ~1000, since many sequences descend by multiple mutations from their closest ancestor. Since lineage A differs by a C→T and one other, coincidentally T→C, if we confine the possibilities to B descended from A and A from B, the odds for B from A are P(non-reversionary (C→T & other))/P(reversionary (C→T & other)). Using that C→T mutations account for roughly half of all the mutations, this ratio becomes about (1/2)(1/2)/((1/25)(1/250)) = ~1500/1. This result is slightly larger than what we found without distinguishing between different types of reversions or considering the frequencies of each type. Thus following Pekar et al. to distinguish between C→T and other reversions supports the case that a pure B spillover is highly improbable.
One sequence listed (MKAK-CL-2020-6430) differs from B by only 4 reversions, 2 C→T’s and 2 others. The probability that if B were the MRCA any of the 787 early sequences shown would have a difference of that sort is in the ballpark of
787*(4 choose 2)*(41/1000)2(4/1000)2 = ~1.5*10-4. Even allowing for the post-hoc choice of features, i.e. some potential multiple comparisons, this is a low probability. If lineage A were the MRCA, the expectation value of the number of sequences meeting those criteria would be ~787*(2 choose 1)*(41/1000)(4/1000) = ~0.3, so finding one would be entirely unremarkable.
Once again, including Pekar et al.’s emphasis on the special role of C→T reversions makes a pure-B spillover even less plausible. Although their case for a high probability of two spillovers disintegrates under inspection, there’s no particular reason to say that two spillovers have a very low probability and thus no phylogenetic reason to discount the possibility of an HSM spillover much further. The tiny fraction of the wildlife trade that went through Wuhan gives a much larger factor without any subtle complications.
Pekar et al.’s reversion statistics also help make the Sangon sequences more interesting. The probability that of the 14 Sangon mutations (relative to lineage B) at least 2 would be C→T reversions and at least 1 another reversion is only ~1%. (If any are just misreads, that percentage drops further.) The probability that those 3 reversions would exactly match the Kumar MRCA rather than other 20 known early reversions is of course lower, somewhere in the vicinity of 10-5 if each C→T and each other reversion is equally likely. That dramatic match cannot be fully explained simply by saying that the earliest mutations determined Kumar’s choice of MRCA since in order to avoid distortion from time-dependent ascertainment probability the Kumar modeling explicitly did not use the observation dates of early sequences. I’m not sure how much these considerations would weigh in deciding if Sangon had a lab MRCA or a collection of very early clinical sample cultures. They are clearly inconsistent with a unique B spillover.
A recent talk by Worobey repeated the Pekar et al. errors and added an additional fundamental one. He described their calculated probability of two spillovers as having been 99.5%, i.e. 200/1 odds. Actually the paper itself, on which he was a coauthor, had originally given 60/1, with his 200/1 apparently coming from just using one likelihood rather than from taking a ratio, a truly fundamental error. He then corrected those odds to 30/1, i.e. acknowledging the factor of 6 coding error but sticking with the fundamental misunderstanding of how to get odds from likelihoods. He included no correction for either of the other two acknowledged coding errors, for the peculiar priors, or for the unbalanced outcome requirements for the two hypotheses. In the bulk of the talk, focussing on location data, no mention was made of the early Weibo map or other evidence undermining the argument for or even contradicting the HSM account.
This talk is important not for our odds calculation but rather for understanding the level of alleged science underlying the canonical account. Whatever may become of my odds estimates in the light of new evidence and new reasoning, the conclusion should hold that the key arguments on which the zoonotic view currently rests are shoddy at best.
Appendix 3: Calculations
The calculations here are not intended to imply unrealistic precision. They are meant simply to use defined logical algorithms to avoid unnecessarily adding even more subjective steps.
To estimate the expected ln(likelihood) and its variance for an event based on observing it M times out of N trials, I subjectively assume a uniform prior on the probability, x, for not finding a host when there actually is one, giving analytically solvable integrals:
For N=2, M=0 we get <ln(likelihood)> = -1.67 with standard error of 1.59.
For N=4, M=1 we get <ln(likelihood)> = -1.28 with standard error of 0.68.
For N=7, M=2 we get <ln(likelihood)> = -1.22 with standard error of 0.53.
(I just found out that this particular exercise is close to the first posthumously published example worked out by Bayes.)
For the restriction enzyme segment pattern I tried a quick sanity check on the probability of randomly getting Nseg=6 with maxL<8knt by assuming a Poisson distribution of the number of sites (Nseg-1) with locations drawn independently from a uniform distribution. Fine-tuning the expectation value of Nseg to be 6 leaves its Poisson probability to be ~1/5. For the probability of then getting small enough maxL I wrote a simulation R program:
> for(j in c(3:10)){tot=0
+ for(i in c(1:1000000)) {vx=sort(runif(j,0,1))
+ if(max(c(vx,1)-c(0,vx))<0.268){tot=tot+1}
+ i=i+1}
+ j=j+1
+ print(c("Nsegments=",j,"fraction=",tot/(i-1)),quote=FALSE)}
1] Nsegments= 4 fraction= 0.000373
1] Nsegments= 5 fraction= 0.013297
[1] Nsegments= 6 fraction= 0.05618
[1] Nsegments= 7 fraction= 0.130738
[1] Nsegments= 8 fraction= 0.227818
[1] Nsegments= 9 fraction= 0.335443
[1] Nsegments= 10 fraction= 0.440921
[1] Nsegments= 11 fraction= 0.539441
With only about 5.6% chance of having maxL be small enough, one ends up with P(6, <8knt)=~1/100. This crude calculation, making no use of the known relatives and allowing fine-tuning to maximize P(6) again indicates that our Bayes factor for this feature is conservative.
Likelihood weighting and final odds
At several steps we need to convert a distribution of logs of probability ratios to net odds. This is the key step in down-weighting likelihood ratios to take into account uncertainty and in combining the distribution of plausible priors with the net likelihood ratio to get the net odds.
For each likelihood ratio we can represent the uncertainties by a nuisance parameter qi with a prior probability density function f(qi) with mean of zero and standard deviation si = Vi1/2 such that in a hypothetical perfectly specified model
ln(P(obsi|LL)/P(obsi|ZW)) = Li+ qi. These uncertainties are important because our logit is the log of the likelihood ratio obtained from averaging probabilities over the distribution, which is not the average of the log of the likelihood ratio, Li.
We want a simple weighting function that captures the key qualitative features, going to 1 when Vi = 0, to zero for large Vi, always contributing to the net likelihood with the same sign as Li but never contributing more than Li. The weighting procedure used here will be to calculate the expected odds obtained from the distribution of likelihood ratios starting with prior odds of 1.0. i.e.
There is no reason to think that this weighting procedure is optimal for a general case, but it’s adequate for the fairly small corrections needed here in our crude model.
[Jamie Robins has pointed out that the correction used for uncertainty here is formally correct under some simplifying assumptions if the nuisance parameter for each observation is shared between the likelihoods for the two hypotheses. Usually it would be more realistic to treat the nuisance parameters for each hypothesis as independent so that the integral should be done on each likelihood rather than than on the ratio. I’ve now included notes with each logit on the approximate effect that change would have. The net effect would be to slightly increase the LL odds, but I haven’t bothered to incorporate that slight change in the summary.]
For small Vi the result is only weakly sensitive to the form of the distribution of qi. To lowest order in Vi the effect becomes logiti = Li -0.5* Vi *tanh(Li/2)). For large Vi that lowest-order approximation overstates the correction but the result can be obtained directly from the integrals if a form is assumed for f(qi), e.g. Gaussian or uniform. For a uniform distribution there’s an analytic expression,
ln(ln((1+e(L+s*3^0.5) )/(1+e(L- s*3^0.5)))/ ln((1+e(-L+ s*3^0.5))/(1+e(-L- s*3^0.5)))). For the CGGCGG factor I used the same uniform distribution described in the text.
For the last step we combine the prior distribution with the log of the net likelihood ratio, L, the sum of the likelihood logits, to obtain the odds.
To reiterate, our method of taking uncertainties into account reduces the odds favoring LL, both for uncertainties in likelihoods and for uncertainty in the priors.
New Priors
How much does our conclusion that SC2 was almost certainly from a lab change the odds we would give if a similar situation were to show up in the future? We started off with ~70/1 odds favoring some sort of ZW story, but we were quite uncertain about that. We had logit0 =4.2±2.3. Now we can treat that as a continuous distribution of hypotheses about what the best prior odds should have been, expressed as a distribution on x, the log of the odds. We re-evaluated that distribution in light of an observation, using that usual Bayesian likelihood ratios. The observation is our the conclusion that SC2 came from a lab. The very small chance that it didn’t will have negligible effect on the resulting calculation, which is obviously very rough anyway.
For any x the likelihood P(LL|x) remains 1/(1+e-x). Then
Let’s recognize the limits of our knowledge by using for the prior our fat-tailed 3-d.o.f. t-distribution with mean of -4.2 and s of 2.3 that allowed a chance of ~1/300 of ZW:
Simply plugging that into the integral gives a posterior distribution for x with mean of -0.50 and s of 3.1. The starting prior and the one to use next time are illustrated here, with the new one on the right. The x-axis is the natural log of the odds.
Appendix 4: FCS uses
The FCS appears at several points in the argument, so it may help to clarify in what ways it is used and in what ways it isn’t used.
Although some have argued that having an FCS is very unlikely for this type of coronavirus, that low likelihood may not apply when one remembers the precondition that we wouldn’t be discussing this virus if there weren’t a pandemic for which the FCS may be nearly needed. Now I’ve modified that restraint somewhat because many non-bat species host sarbecoviruses without any FCS even though having an FCS seems evolutionarily advantageous for the respiratory versions outside bats.
The detailed contents of the FCS, the CGGCGG sequence, provide one significant piece of evidence used, since it seems P(CGGCGG|LL) is larger than P(CGGCGG|ZW). On the fuzzy issue of what codons to expect in a synthetic sequence, if the LL codon choice for ArgArg were purely random, we’d have P(CGGCGG|LL)=1/36. When sequences are synthesized for use in hosts, however, they are typically “codon optimized”, using the more common host codons, such as CGG in humans, even more frequently than they are found in the host. CGG codes for 20% of human Arg. Thus a reasonable first minimum estimate of P(CGGCGG|LL) would be 0.22=0.04. More likely, since the two rarer codons would generally not be used, a good low estimate would be (1/4)2=0.06.
I found two convenient relevant examples of how often CGG would be used in modern RNA synthesis for human hosts, specifically of stretches coding for portions of the SC2 spike protein used in the Pfizer and Moderna vaccines. Both mRNA vaccines and viral genomes need to be stable in the host organism and to work well at highjacking the host machinery to generate the proteins for which they code, so there’s quite a bit of overlap in the criteria used in choosing codons.
Unlike vaccine mRNA, however, viral RNA also needs to replicate well and to pack well into the viral package. For our purposes, looking at just a few nt on an insert that already disrupts the previous RNA structure, packing is probably irrelevant. Is there any indication that CGG is thought to be a particularly poor replicator in humans, in which case we should lower our estimate of P(CGGCGG|LL) compared to what’s found in mRNA vaccines? In the years since SC2 started, almost all strains remain CGGCGG, although some synonymous mutations to CGUCGG are now present. Thus there is no indication that a viral sequence designer would have any special reason to avoid CGG for reproductive reasons, so the vaccine coding can give us a rough idea of how likely a CGGCGG choice would be for a synthetic viral sequence.
CGG is used far more often in the Pfizer and Moderna vaccines than in the natural viruses: “The designers of both vaccines considered CGG as the optimal codon in the CGN codon family and recoded almost all CGN codons to CGG.” 19 of 41 Arg codons in Pfizer are CGG, as are 39 of 42 in Moderna. The designers were not inspired to use CGG by its appearance in the FCS on the target protein, since none of the other 40 Arg’s on that protein use CGG. Deigin has pointed out another reason that a researcher inserting coding for ArgArg might specifically choose CGGCGG— it provides a marker for a standard, easy, restriction enzyme test allowing the researcher to know if that insertion is still present or has been lost, an important consideration since FCS’s tend to get lost in cell culture. (AGGCGG would also code for ArgArg and work for the marker.) On the other hand, although both designers were fond of CGG, neither used CGGCGG for the ArgArg pair, indicating that they had some reason to avoid it, perhaps connected to occasional translational errors that might be particularly important to avoid in vaccines although less important for viral fitness. The |LL) likelihood factor here may go up or down if I can track down why the vaccine designers chose not to use CGGCGG.
The amino acid sequence of the SC2 FCS is identical to a familiar human amino acid sequence that would be a good candidate for use in a furin cleavage site promoting infectivity. In that human FCS sequence the ArgArg pair is coded CGUCGA, which would become CGGCGG either under the choice CGN—>CGG usually used by vaccine coders or to implement the standard tracing procedure described by Deigin.
In the one example of which I’m aware in which a collaborator of the WIV group added a 12nt code for an FCS to produce a viral protein via a plasmid (reminiscent of the 12nt addition in SC2) they only used CGG for one of its three Arg’s. Other plasmid primers from WIV use high fractions of CGG, including CGGCGG dimers, but again these are for plasmid work and thus subject to substantially different optimization criteria.
We can check that we have not missed some important argument that CGG would be disfavored in a lab by reading Andersen’s extensive argument that CGG did not indicate LL. While presenting detailed non-statistical scenarios of how CGG might possibly arise naturally, it makes no mention of any reasons why it might be disfavored in a lab.
Wuhan is not the only place where pathogen research is done, so a priori it would be an exaggeration to say P(Wuhan|LL, pandemic) = ~1. However, the combination of the DEFUSE proposal to add an FCS to coronaviruses, along with other DEFUSE proposed features found, strongly indicate that if SC2 originated from a lab, it would be one doing the DEFUSE-proposed work. The site mentioned in DEFUSE for adding an FCS to a coronavirus, UNC, is smaller and uses highly enhanced BSL3 protocols. After DEFUSE was not funded, switching this part of the work to WIV, where there was already expertise in the methods, would have been easy. A note from a lead investigator, Peter Daszak, to the NIH about earlier work had assured them in 2016 that “UNC has no oversight over the chimera work, all of which will be conducted at the Wuhan Institute of Virology.” Notes from DEFUSE investigators have recently been released describing plans to actually conduct much of the research described as planned for BSL3 at UNC instead in Wuhan, where BSL-2 was often used. While the chance of a spillover occurring at UNC isn’t zero, it’s much lower than for WIV. Thus
P(Wuhan|LL, coronavirus with FCS, etc.) = ~1.
Deigin points out that FCS in SC2 occurs exactly at the S1/S2 junction, an obvious place for a DEFUSE-style insertion. A recently released early draft of DEFUSE (before compression to meet space limits) specifically mentions the S1/S2 boundary as a target for a cleavage site insertion, by sequence location number rather than by name. Since that is also, not coincidentally, an evolutionarily advantageous location, it might only provide a small update factor favoring LL, which I don’t use.
The S2 neighborhood of the FCS, differing from related viruses only by synonymous mutations, has been cited as evidence for LL because it looks peculiar under ZW but not under LL, as in the Garry quote above. The initial post-spillover strains lacked a mutation called D614G that becomes advantageous specifically to compensate for some effects of the FCS. D614G arose quickly to predominate in multiple lines of SC2 as it spread in humans. The combination of the FCS coding, the lack of amino acid changes in S2, and the initial absence of D614G all indicate that the outbreak started not very long after the FCS was inserted, whether naturally or in a lab.
The picture of a quick route to human spillover after FCS insertion is easily consistent with LL. It fits well with only a particular subset of the zoonotic hypothesis.
Appendix 5: Research spillover of a zoonotic virus
So far I have just ignored the ZL account of a virus that formed naturally but successfully spilled over into humans via research activities. For origins via an intermediate host including ZL would just add another research channel increasing the lab vs. zoonotic odds. The sequence evidence indicates that some modification probably occurred in the lab, so including ZL wouldn’t change those odds much. Although the likelihood factors from the FCS coding and the restriction enzyme pattern strongly favor lab modification, it’s worth having a quick look at the P(ZL)/P(ZW) odds for accounts lacking an intermediate host, especially since there’s some chance that SC1 lacked an intermediate host.
Several of the features that we have noted could fit together in a zoonotic picture qualitatively different from the bat—>wildlife—>market—> human version usually considered. The evidence described in Appendix 4 requires there was only a short interval between the FCS insertion and the spillover, perfectly consistent with LL but perhaps also with a particular zoonotic account along the direct-from-bats lines that Wenzel proposed for SC1.
The reports of Laotian BANAL bat sarbecoviruses with good human ACE2 binding but lacking an FCS suggest a way for getting good preadaptation while skipping intermediate wildlife hosts altogether. Someone in Laos could have become directly infected with a BANAL-related bat virus that contained a small trace of FCS variants, too little to detect in consensus sequencing tests, before those variants were lost due to their lack of fitness in bats. Likewise an accidental FCS insertion could have occurred in the person before the virus was eliminated. With some luck, the virus might survive long enough for those few FCS-containing virions to become the main strain in the human host. The disintegration of the evidence for an HSM spillover would not be surprising in this zoonotic story, since HSM would have no initial role to play.
The direct-from-bat accounts (whether natural or via research) require wending an especially narrow path to spillover needing an FCS insert and a properly ablated N-linked glycan to appear almost simultaneously in a virus that already happened to have an RBD well-adapted to humans. The absence of any FCS-containing sarbecoviruses in any host species, including humans, indicates that such coincidences would be rare even after considering post-selection for successful replication outside bats. It would be worth further investigating the occasional successful spillovers from bats. Thus I do not think that the ZWB account is nearly as probable as the LL one that there was a leak from DEFUSE-like work, perhaps being done using a BANAL-related pre-FCS backbone.
If a direct spillover from a bat or an unmodified sample from a bat did nonetheless occur, the remaining issue would then be how the virus got from Laos or nearby to Wuhan without leaving a trace. This is where ZL accounts become most relevant.
For P(ZL)/P(ZW) odds we can start with Demaneuf and De Maistre’s analysis, predating DEFUSE and some other relevant evidence. Their base estimate, using their best estimates of lab leak probabilities and non-research probabilities
P(ZL|Wuhan)/P(ZW|Wuhan) = ~4. They also include a conservative estimate, 1.2, using factors tilted toward ZW compared to their best estimates and a “de minimis” estimate using the most extreme estimated factors, giving 1/15. Rather than reproduce the whole careful analysis it makes sense to consider what incremental changes should be made based on information that has become available since their work.
Several factors have become clearer. Better sampling of related viruses has now shown that if the SC2 chimera arose in nature it would almost certainly have to have happened in southern Yunnan or farther south in or near Laos. That lowers the chance of showing up first in Wuhan compared to Demaneuf and De Maistre’s analysis, which allowed some chance for the virus to have originated closer to Wuhan. Their zoonatic possibilities also included transmission via intermediate hosts, but we have already included that possibility elsewhere. (At any rate, it has lower probability than Demaneuf and De Maistre’s analysis cautiously assumed because as we’ve seen Wuhan has a much lower share of the wildlife trade than expected from the population. )
The continued absence of any detected intermediate host, including any human hosts, between the possible spillover and Wuhan plays the about same role in enhancing the odds for ZL vs. ZW as it does for LL. ZL could provide a simple one-step route for the virus getting from a possible spillover source in or near Laos to Wuhan since in Aug. 2019 WIV and Daszak submitted a publication describing the partial sequence of a bat coronavirus they had gathered in Laos. That publication had not been noticed at the time of Demaneuf and De Maistre’s analysis. The research team had received authorization to continue such sampling. A researcher could have been infected while gathering samples or after bringing samples back to Wuhan.
The original estimates assumed that work was done at BSL-3. We now know that much of the lab work was to be done at BSL-2. That raises the ZL odds.
Dropping the already-counted market routes that provided the main way a zoonotic infection could arrive in Wuhan without leaving a human trail, allowing for the acknowledged BSL-2 work, using the more definite information that the source of a direct bat infection would have had to be at least as far south as southern Yunnan, and adding documented sampling in that region by Wuhan researchers all raise the odds that a direct-from-bats sarbecovirus infection would have arrived in Wuhan via research rather than via some other route. I think the straight Bayes odds (not integrating over uncertainty in parameters) would then go up from ~4/1 to well over 10/1. Allowing for uncertainties would pull that back part way toward 1. ZLB seems substantially more probable than ZWB even though some of the factors pointing toward LL (CGGCGG, pre-adaptation, and lack of detected intermediate hosts) are not relevant to that comparison. Since the sequence data make any direct-from-bats route fairly unlikely to begin with, allowing this possibility would do little to change our net odds. If for some reason all intermediate-host accounts including LL were ruled out, then the odds would still favor a research-related account, but probably not by as much as in our main estimate.
Appendix 6: Future Refinements
Barring some unforeseen release of new evidence that is both highly relevant and highly reliable, pinning down the odds further will require more steady analysis of circumstantial data. It may help to mention some key pieces of information and calculation for which progress is feasible.
Which, if any, of the species available in HSM combined reasonable ability to catch and transmit early strains of SC2, sourcing from southern provinces, and either records of sales in Fall 2019 or traces of DNA from sampling? What fraction of the net Chinese trade in the southern-source part of the species (if any) occurred in Wuhan? At least two people are working on this project. Their results are likely to help pin down the priors for the market version of ZW. Since by far the strongest piece of positive evidence for the ZW according to the recent analyses is dependent on an HSM spillover, tracking down this market-specific prior is particularly important.
How many of the non-bat species with sarbecoviruses lacking an FCS have mainly respiratory transmission? That could raise or lower our uncertain relevance of the missing FCS’s to SC2.
Right now the P(CGGCGG|ZW) is based on an informal calculation of statistics of apparent 12nt inserts from the reliable, careful, but pseudonymous Guy Gadboit. It would be nice to have a more formally available one based on more complete data sets.
Although the mRNA vaccines used lots of CGG, each avoided the one chance to use CGGCGG. Was the reason relevant to viral design? The answer could raise or lower our Bayes factor from the CGGCGG observations.
Although it is not likely to affect our bottom line, it would be nice to see what becomes of the odds for two spillover when that likelihood is calculated using the same observation as used for one spillover rather than a superset.
This is far from an exhaustive list.







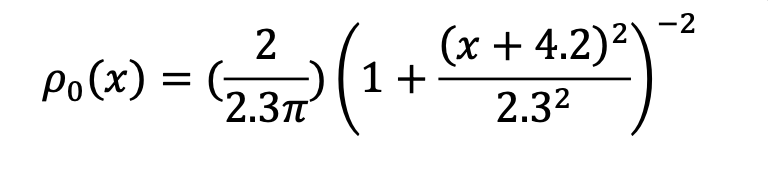
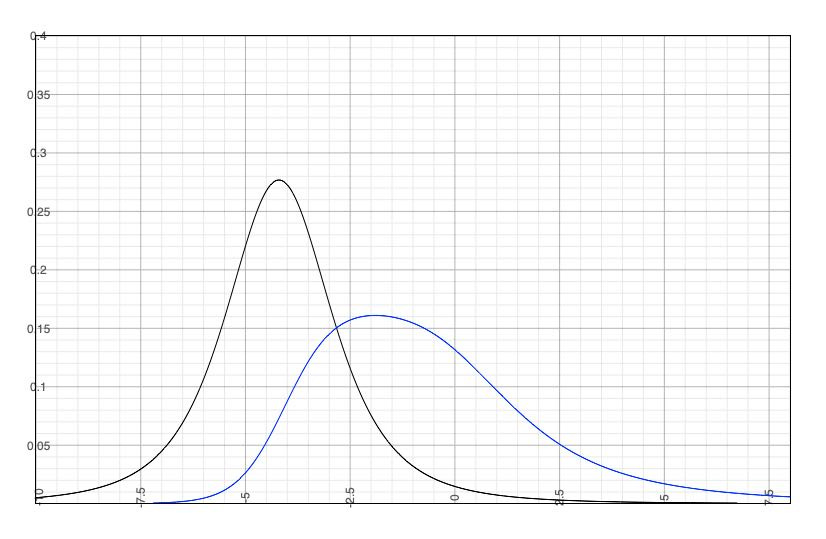
Thank you for this remarkable work. I consider it of great importance to not stop trying to get to the bottom of this. If found the discourse in science, politics, media and social media about vital questions like the origin of covid quite disfunctional. Continuing the debate and correcting errors is a chance for re-establishing trust in science and society as a whole.
I am afraid I have nothing of substance to contribute. I believe public estimates by other entities not backed up by (publicly available) Bayesian analysis would not be relevant. But for what it's worth, Jeffrey Sachs (who headed the Lancet Covid Commission, which had a sub-group looking into Covid origin) mentioned in a recent interview that he estimated the chances of a lab leak at 98-99%. The German secret service is reported to have estimated the likelihood at 80-95%. In both cases, I am not aware of the confidence assigned to this interval. Lothar Wieler, who headed the Robert-Koch-Institute (the German government's central scientific institution in the field of biomedicine) during Covid, has recently stated to the press that he considers "a fabricated virus which leaked from a lab" as the most likely hypothesis without quantifying his statement. When putting this information next to the current Wikipedia article on the origin of covid, it is apparent how utterly disfunctional the public discourse has become.
Hi-- Could you link to my report at https://ermsta.com/covid_debate instead of the link you use, thanks.
I have written a response to some of the things you have written which may clarify a few points: https://ermsta.com/posts/20240301
Cheers